Equations de droites
Définition :
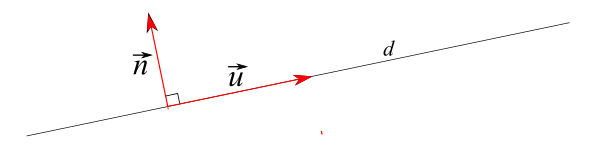
Un vecteur non nul est dit normal à une droite (d) lorsque est orthogonal à un vecteur directeur de la droite (d).
Remarque :
La droite d passant par A et de vecteur normal est l'ensemble des points M tels que .
Propriétés :
• Dans un
repère orthonormé, si une droite
d a pour équation
ax + by + c = 0 (avec
a≠0 ou
b≠0), alors
est un
vecteur normal à
d.
• Dans un
repère orthonormé, si un vecteur non nul
est
normal à
d, alors
d a pour équation
ax + by + c = 0.
Equations de cercles
Propriété 1 :
Soit
le cercle de centre O(
xO;yO) et de rayon R dans un repère orthonormé. Une équation de
est :
(x - xO)² + (y - yO)² = R²
Propriété 2 :
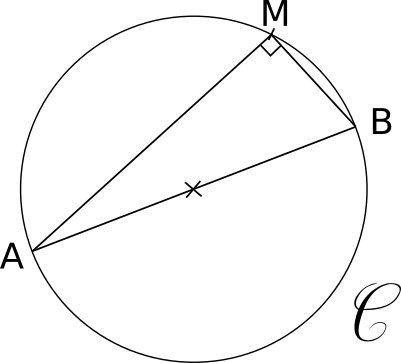
Le cercle
de diamètre [AB] est l'ensemble des points M tels que :
⇔M ∈
Calculs de longueurs et d'angles dans un triangle
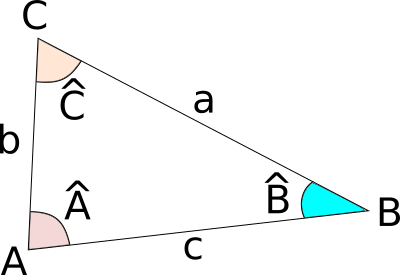
Soit un triangle ABC, on note a = BC, b = AC et c = AB.
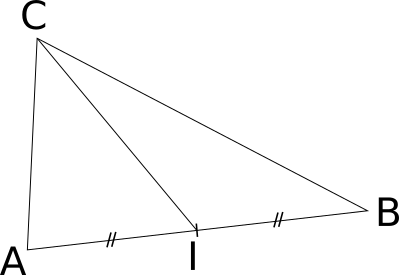
Théorème de la médiane :
Soit I le milieu de [AB], on a :
Théorème d'Al-Kashi :
•
•
•
Propriété de l'aire d'un triangle :
Dans un triangle ABC, d'aire S :
•
•
•
Formule des sinus :
Dans un triangle ABC :
=
=
Formules d'addition et de duplication
Formules d'addition :
Pour tout nombre réel a et b :
•
•
•
•
Formules de duplication :
Pour tout nombre réel a :
•
•
•
