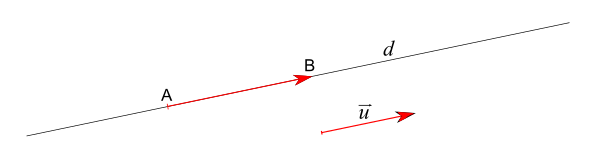
Vecteur directeur d'une droite
Définition :
Soient A et B deux points distincts d'une droite d. Tout vecteur non nul colinéaire à est un vecteur directeur de la droite d. Le vecteur a la même direction que la droite d.
Remarques :
• Soient A et B deux points distincts de d, est un vecteur directeur de d.
• Si est un vecteur directeur de d, alors quel que soit k ≠ 0, est aussi un vecteur directeur de .
Propriété :
Soient et deux vecteurs directeurs respectifs de deux droites d et d'.
Les droites
d et
d' sont parallèles si et seulement si
et
sont colinéaires.
Equation cartésienne d'une droite
Propriété 1 :
Dans un repère, toute droite d du plan a une équation de la forme ax + by + c = 0 .
avec a≠0 ou b≠0. Le vecteur (-b;a) est un vecteur directeur de d.
Propriété 2 :
Dans un repère, l'ensemble des points M(x;y) tels que ax+by+c=0 avec a≠0 ou b≠0 est une droite de vecteur directeur (-b;a).
Définition :
Une équation d'une droite d de la forme ax+by+c=0 avec a≠0 ou b≠0 est appelée équation cartésienne de la droite d.
Exemple : Déterminer une équation cartésienne
Dans un repère, déterminer une équation de la droite d passant par A(2;3) et de vecteur directeur (-4;3).
Solution : d a pour équation ax+by+c=0. Puisque (-4;3) est un vecteur directeur, une equation de d peut s'écrire 3x+4y+c=0.
Or, A(2;3) appartient à d, donc : 3×2+4×3+c = 0, soit 6+12+c=0, d'où c = -18.
d a donc pour équation cartésienne 3x+4y-18=0.
Position relative de deux droites
Propriété :
Soient d et d' deux droites du plan d'équations cartésiennes respectives ax+by+c=0 et a'x+b'y+c'=0 avec a≠0 ou b≠0 et a'≠0 ou b'≠0. Les vecteurs (-b;a) et (-b';a') sont des vecteurs directeurs de d et d'.
Les droites d et d' sont parallèles si et seulement si et sont colinéaires.
Autrement dit les droites d et d' sont parallèles si et seulement si a'b - ab' = 0.
Exemples :
1) Soient d et d' deux droites d'équations respectives x - 2y + 1 = 0 et -3x + 6y - 2 = 0. Les droites d et d' sont elles parallèles ?
Réponse : (2;1) est un vecteur directeur de d et (-6;-3) est un vecteur directeur de d'. = -3, donc et sont colinéaires. Les droites d et d' sont donc parallèles.
2) Soient d et d' deux droites d'équations respectives 2x + y + 4 = 0 et -3x - 2y + 1 = 0. Les droites d et d' sont elles parallèles ?
Réponse : (-1;2) est un vecteur directeur de d et (2;-3) est un vecteur directeur de d'. -1×(-3)-2×2 = 3 - 4 = -1 , donc et ne sont pas colinéaires. Les droites d et d' ne sont donc pas parallèles.