Notion de vecteur
Vecteurs et translation :
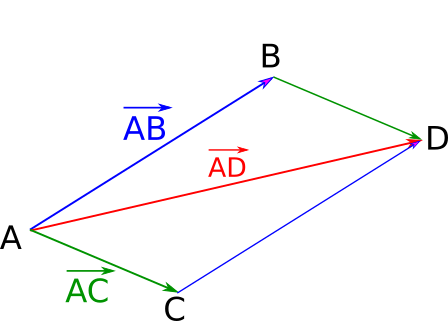
Soit A et B deux points distincts du plan. La translation qui transforme A en B associe à tout point C du plan, l'unique point D tel que les segments [BC] et [AD] ont le même milieu.
Cette translation est appelée la translation de vecteur
Exemple : (clique sur le bouton en bas à droite pour faire défiler l'animation)
Caractérisation d'un vecteur :
Un vecteur est caractérisé par sa direction, son sens et sa longueur. On le représente par une flèche. On peut le noter
, , ... ou , ... où A, B, M et N sont des points du plan.
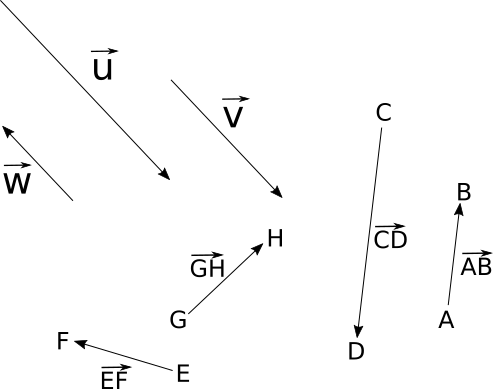
Exemples :
Attention à ne pas confondre sens et direction ! Ici,
et ont même direction et même sens alors que et ont la même direction mais des sens contraires.
Attention aussi à l'ordre des lettres lorsqu'on nomme un vecteur ! La première lettre est toujours l'origine du vecteur. Ici, les vecteurs et ont la même direction mais des sens contraires.
Norme d'un vecteur :
La longueur d'un vecteur s'appelle la norme de et se note
Vecteurs égaux :
Deux vecteurs sont égaux si ils ont la même direction, le même sens et la même norme. Cela signifie que si deux vecteurs et sont égaux, alors le quadrilatère ABDC est un parallélogramme (Attention à l'ordre des lettres ! Il s'agit du quadrilatère ABDC et non ABCD.)
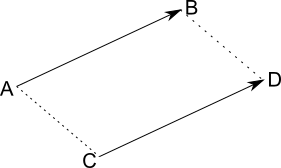
Exemple :
.
ABDC est un parallélogramme.
Opposé d'un vecteur :
Le vecteur opposé au vecteur est un vecteur de même direction et de même norme que mais de sens opposé. On le note . L'opposé du vecteur est le vecteur
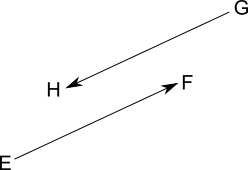
Exemples :
et
ont même direction, même norme mais des sens opposés donc est un vecteur opposé au vecteur .
On peut écrire :
Vecteur nul :
On appelle vecteur nul le vecteur qui a une norme égale à 0. On le note . Il n'a ni sens, ni direction.
Quel que soit le point A du plan,
Coordonnées d'un vecteur
Définition :
Dans un repère (O; I,J) les coordonnées d'un vecteur sont les coordonnées du point M tel que .
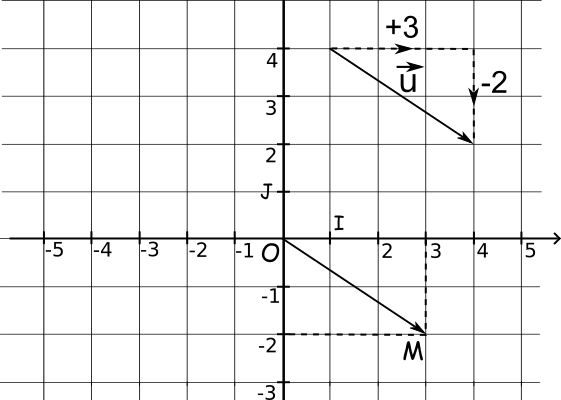
Exemples :
donc le vecteur
a pour coordonnées (3 ; -2).
On peut noter = (3 ; -2) ou
En pratique, on peut compter les carreaux en commençant par l'origine du vecteur, en se déplaçant sur l'axe des abscisses, puis sur l'axe des ordonnées pour arriver jusqu'à la pointe de la flèche.
Coordonnées du vecteur :
Dans un repère (O; I,J), si et , alors le vecteur a pour coordonnées
Exemples :
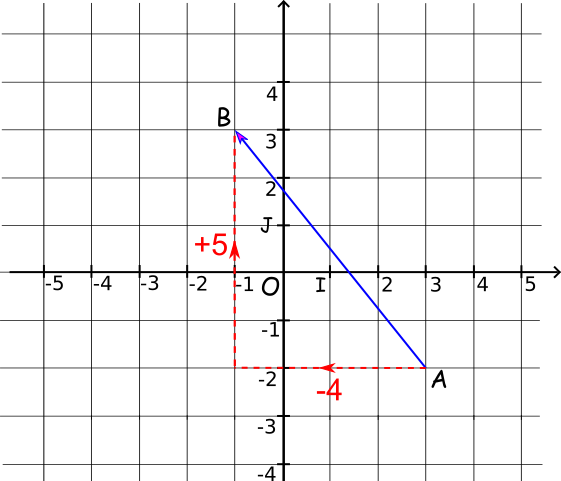
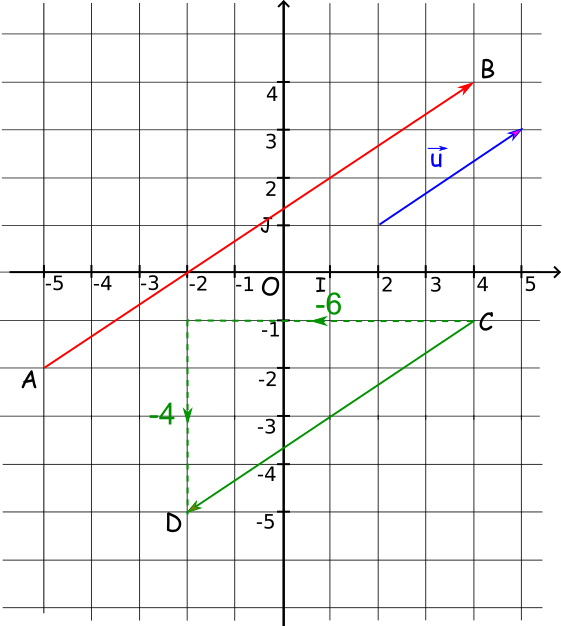
et .
Donc , donc
On peut vérifier graphiquement que pour aller de A à B, on se déplace de -4 en abscisse, puis de +5 en ordonnées, d'où
Propriété :
Deux vecteurs sont égaux si et seulement si ils ont les mêmes coordonnées dans un repère du plan.
Somme de deux vecteurs
Définition :
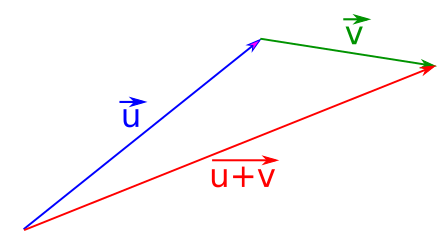
En effectuant successivement une translation de vecteur et une translation de vecteur , on obtient une nouvelle translation. Le vecteur associé à cette translation est le vecteur .
Remarque :
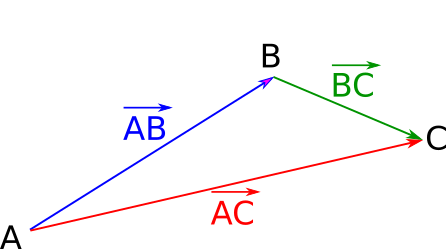
Relation de Chasles :
Quels que soient les point A, B et C du plan, on a :
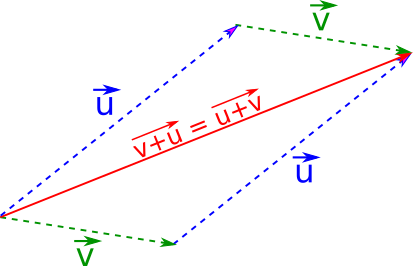
Règle du parallélogramme :
Soient les point A, B, C et D quatre points du plan.
ABDC est un parallélogramme si et seulement si
Propriété :
Soient et
deux vecteurs du plan.
Le vecteur a pour coordonnées .
Exemple :
Si
et
, alors
, donc
Opposé d'un vecteur, différence de deux vecteurs :
Si
et
, alors
et
.
Multiplication d'un vecteur par un nombre réel
Définition :
Soient k un nombre réel, et dans un repère du plan. Le vecteur est le vecteur de coordonnées dans le même repère.
Exemples :
.
, donc , donc .
, donc , donc .
Propriétés :
Soient k et k' deux nombres réels, et et deux vecteurs du plan.
(k + k') = k + k'
k (k') = (k k')
k ( + ) = k + k