Raisonnement par récurrence
Démonstration par récurrence :
Le raisonnement par récurrence est utilisé pour démontrer qu'une propriété est vraie pour tous les entiers n à partir d'un certain rang n
0.
On procède par étapes :
• Initialisation : on vérifie que la propriété est vraie au rang n
0.
• Hérédité : on vérifie que si la propriété est vraie à un certain rang
k, alors elle est vraie au rang
k+1.
• Conclusion : la propriété est vraie au rang n
0 et est héréditaire, elle est donc vraie pour tout n≥n
0
Exemples :
1) Soit (U
n) la suite définie par U
0=5 et U
n+1=0,5U
n+4. Montrer par récurrence que U
n≤8 pour tout n≥0.
• Soit P(n) = «U
n≤8»
•
Initialisation : U
0=5 et 5≤8 donc P(0) est vraie.
•
Hérédité : Supposons que P(k) soit vraie pour un certain entier k≥0. On a alors :
Uk ≤ 8
0,5Uk ≤ 0,5×8
0,5Uk+4 ≤ 0,5×8+4
Uk+1 ≤ 8
donc P(k+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=0 et est héréditaire, donc par récurrence elle est vraie pour tout n≥0 et U
n≤8 pour tout n≥0.
2) Soit (V
n) la suite définie par V
0=1 et V
n+1=2V
n+3. Montrer par récurrence que V
n=2
n+2-3 pour tout n≥0.
• Soit P(n) = «V
n=2
n+2-3»
•
Initialisation : V
0=1 et 2
0+2-3=2
2-3=4-3=1 donc P(0) est vraie.
•
Hérédité : Supposons que P(k) soit vraie pour un certain entier k≥0. On a alors :
Vk = 2k+2-3
Vk+1 = 2(2k+2-3)+3
Vk+1 = 2k+3-6+3
Vk+1 = 2k+3-3
donc P(k+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=0 et est héréditaire, donc par récurrence elle est vraie pour tout n≥0 et V
n=2
n+2-3 pour tout n≥0.
3) Montrer par récurrence que pour tout entier n≥1,
.
• Soit P(n) = «
»
•
Initialisation : et
donc P(1) est vraie.
•
Hérédité : Supposons que P(n) soit vraie pour un certain entier n≥0, on veut montrer que P(n+1) est vraie.
P(n+1) = «
»
Si P(n) est vraie, on a alors :
donc P(n+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=1 et est héréditaire, donc par récurrence elle est vraie pour tout n≥1 et
pour tout n≥1.
Etude du sens de variation d'une suite par récurrence
Rappels :
Pour étudier le
sens de variations d'une suite, on peut :
• étudier le signe de u
n+1 - u
n
• comparer le quotient
à 1 lorsque les termes de la suite sont
strictement positifs
• étudier le sens de variation de f si u est définie par u
n = f(n).
Lorsque la suite est définie par une relation de récurrence du type u
n+1 = f(u
n), les méthodes précédentes ne permettent pas toujours de déterminer son sens de variation. On peut alors utiliser le raisonnement par récurrence.
Méthode :
• On peut montrer qu'une suite est
croissante en montrant par récurrence que u
n+1≥u
n pour tout n∈ℕ
• On peut montrer qu'une suite est
décroissante en montrant par récurrence que u
n+1≤u
n pour tout n∈ℕ
Exemple :
Soit (U
n) la suite définie par U
0=3 et U
n+1=3U
n-4. Montrer par récurrence que (U
n) est croissante.
• Soit P(n) = «U
n+1 ≥ U
n»
•
Initialisation : U
0=3 et U
1=3×3-4=5 donc U
1 ≥ U
0 donc P(0) est vraie.
•
Hérédité : Supposons que P(k) soit vraie pour un certain entier k≥0. On a alors :
Uk+1 ≥ Uk
3Uk+1 ≥ 3Uk
3Uk+1-4 ≥ 3Uk-4
Uk+2 ≥ Uk+1
donc P(k+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=0 et est héréditaire, donc par récurrence elle est vraie pour tout n≥0 et U
n+1 ≥ u
n pour tout n≥0, donc la suite (U
n) est croissante.
Remarque : le sens de variation d'une suite dépend de la valeur de son terme initial. Par exemple, si le premier terme de (U
n) était égal à 1, on aurait : U
0=1 et U
1=-1 donc U
0 ≥ U
1. Avec un raisonnement par récurrence, on constate que (U
n) serait décroissante.
Suites minorées, majorées, bornées :
Définitions :
• Une suite (U
n) est
majorée par un nombre réel M si U
n ≤ M pour tout n∈ℕ. M est appelé un
majorant de la suite (U
n).
• Une suite (U
n) est
minorée par un nombre réel m si m ≤ U
n pour tout n∈ℕ. m est appelé un
minorant de la suite (U
n).
• Une suite (U
n) est
bornée lorsqu'elle est à la fois majorée et minorée.
Exemples :
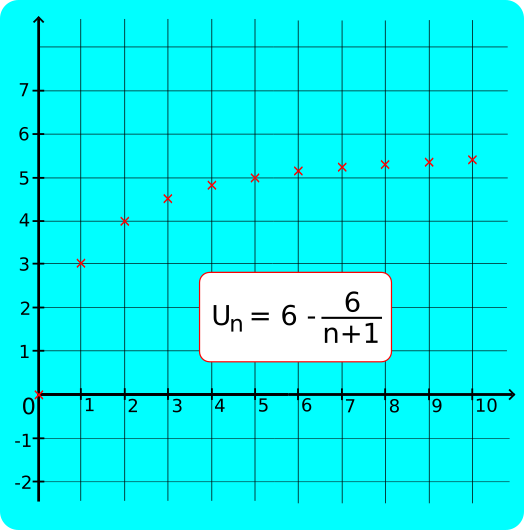
1) Soit (U
n) la suite définie pour tout entier n≥0 par U
n=
.
D'après la représentation graphique, (U
n) semble bornée par 0 et 6.
En effet, pour tout entier naturel n , on a:
n ≥ 0
n+1 ≥ 1
0 ≤ ≤ 1
0 ≤ ≤ 6
-6 ≤ ≤ 0
0 ≤ ≤ 6
0 ≤ Un ≤ 6
Donc la suite (U
n) est bien bornée par 0 et 6.
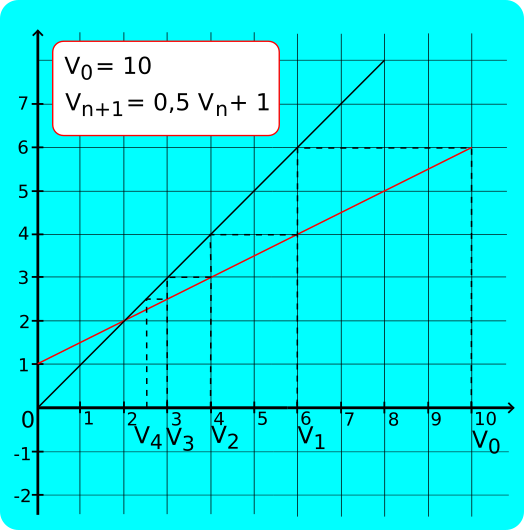
2) Soit (v
n) la suite définie par V
0=10 et pour tout entier n≥0 par V
n+1=0,5 V
n + 1.
D'après la représentation graphique, (V
n) semble bornée par 2 et 10.
Nous allons le démontrer par récurrence :
• Soit P(n) = «2 ≤ u
n ≤ 10»
•
Initialisation : V
0=10 donc P(0) est vraie.
•
Hérédité : Supposons que P(k) soit vraie pour un certain entier k≥0. On a alors :
2 ≤ Vk ≤ 10
2×0,5 ≤ 0,5 Vk ≤ 10×0,5
1 ≤ 0,5 Vk ≤ 5
2 ≤ 0,5 Vk+1 ≤ 6
2 ≤ Vk+1 ≤ 10
donc P(k+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=0 et est héréditaire, donc par récurrence elle est vraie pour tout n≥0 et 2 ≤ V
n ≤ 10 pour tout n≥0, donc la suite (v
n) est bien bornée de 2 à 10.
Remarques :
• Si une suite est majorée par un nombre réel M, alors tous les nombres supérieurs à M sont également des majorants de cette suite.
• Si une suite est minorée par un nombre réel m, alors tous les nombres inférieurs à m sont également des minorants de cette suite.
Propriétés :
• Si une suite est
croissante, alors elle est
minorée par son premier terme.
• Si une suite est
décroissante, alors elle est
majorée par son premier terme.
Exemples :
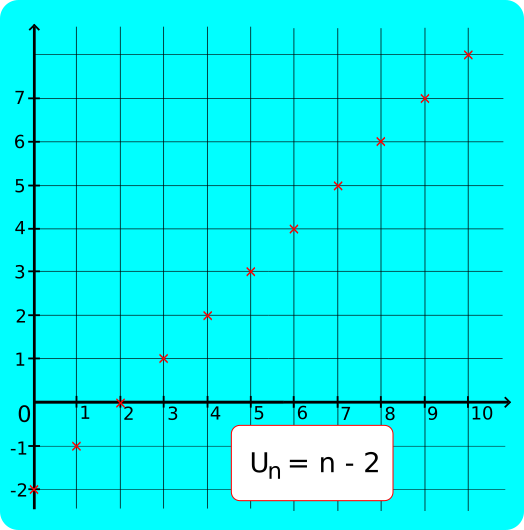
1) Soit (Un) la suite définie pour tout entier n≥0 par Un=n-2.
Un=f(n) avec f la fonction définie sur [0; +∞[ par f(x) = x - 2. f est croissante, donc la suite (Un) est croissante. Or U0 = -2, donc la suite (Un) est minorée par -2.
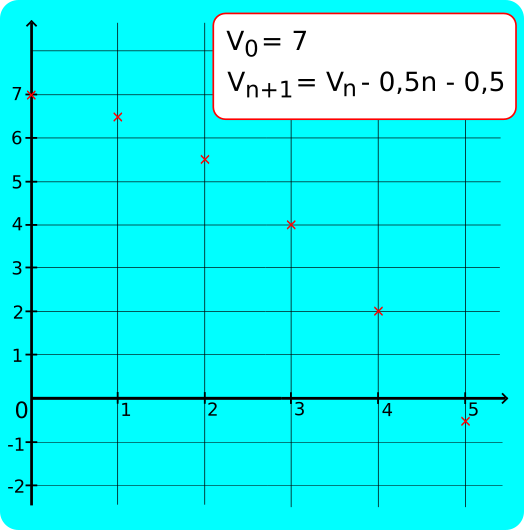
2) Soit (Vn) la suite définie par V0=7 et pour tout entier n≥0 par Vn+1=Vn-0,5n-0,5.
Vn+1-Vn=-0,5n-0,5<0 donc la suite (Vn) est décroissante. Or V0 = 7, donc la suite (Vn) est majorée par 7.