Cours de maths : Limites de suites
Définitions des limites
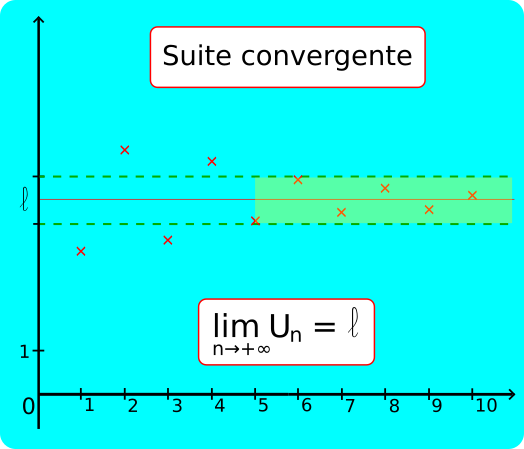
Suites convergentes :
Soit l un nombre réel. Une suite (Un) a pour limite l quand n tend vers +∞ lorsque tout intervalle ouvert contenant l contient toutes les valeurs de (Un) à partir d'un certain rang.
On note alors
l
et on dit que la suite (Un) est convergente vers l.
Cela signifie que pour tout nombre réel r>0, il existe un rang n0 tel que pour tout n≥n0, |Un-l|<r
Propriété :
Une suite convergente admet une
unique limite.
Démonstration : Nous allons procéder par l'absurde. Soit (U
n) une suite convergente. Supposons qu'il existe deux nombres réels
l et
l' tels que
l<
l' et
l et
l'. Posons a=
.
l, donc il existe un entier naturel n
1 tel que pour tout n≥n
1, U
n∈]−∞;a[.
l, donc il existe un entier naturel n
2 tel que pour tout n≥n
2, U
n∈]a;+∞[.
Soit n
0=max(n
1,n
2). Pour tout n≥n
0, U
n∈]−∞;a[∩]a;+∞[, or ]−∞;a[∩]a;+∞[ = Ø, donc l'hypothèse de départ est fausse et la suite (U
n) ne peut avoir deux limites distinctes
Exemple :
Soit (U
n) la suite définie pour tout entier n≥0 par U
n=
. Montrer que (U
n) converge vers 3.
Solution :Soit r>0. On cherche un rang n
0 à partir duquel |U
n-3|<r, c'est à dire |
|<r soit |
|<r c'est à dire
<r car n>0, d'où n+1>
, soit n>
-1.
Soit n
0 un entier supérieur à
-1, pour tout n≥n
0, |U
n-3|<r. Donc
Suites divergentes :
Définitions :
• Une suite qui n'est pas convergente est
divergente.
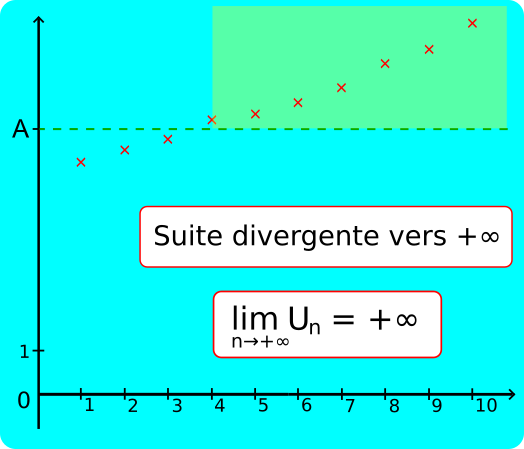
• Une suite (Un) a pour limite +∞ quand n tend vers +∞ lorsque quel que soit le réel A, Un ≥ A à partir d'un certain rang.
On note alors
+∞
Cela signifie que quel que soit le nombre réel A>0, il existe un rang n0 tel que pour tout n≥n0, Un ≥ A
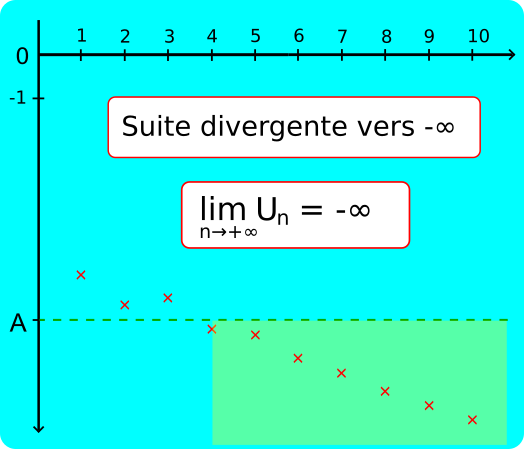
• Une suite (Un) a pour limite −∞ quand n tend vers −∞ lorsque quel que soit le réel A, Un ≤ A à partir d'un certain rang.
On note alors
−∞
Cela signifie que quel que soit le nombre réel A>0, il existe un rang n0 tel que pour tout n≥n0, Un ≤ A
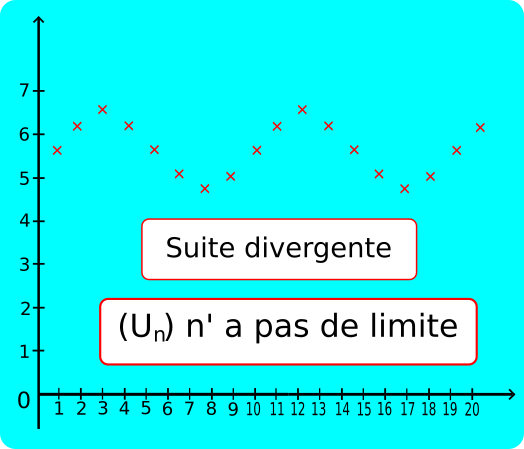
• Une suite (Un) divergente peut ne pas avoir de limite.
Exemples : , , , etc...
Limites usuelles :
•
+∞,
+∞, et
+∞ pour k∈ℕ*
•
0,
0, et
0 pour k∈ℕ*
Opérations sur les limites
Soit
l et
l' deux nombres réels. Le symbole ±∞ signifie «soit +∞ soit −∞». Le sigle F.I signifie «Forme Indéterminée», c'est à dire qu'on ne peut pas conclure.
Somme de limites :
| | l | l | l | +∞ | +∞ | −∞ |
| | l' | +∞ | −∞ | +∞ | −∞ | −∞ |
| | l+l' | +∞ | −∞ | +∞ | F.I. | −∞ |
Produit de limites :
| | l | l>0 | l>0 | l<0 | l<0 | ±∞ | 0 |
| | l' | +∞ | −∞ | +∞ | −∞ | ±∞ | ±∞ |
| | l×l' | +∞ | −∞ | −∞ | +∞ | ±∞ | F.I. |
Quotient de limites :
| | l | l | ±∞ | ±∞ | l≠0 | ±∞ | 0 |
| | l'≠0 | ±∞ | l'≠0 | ±∞ | 0+ ou 0− | 0+ ou 0− | 0 |
|
|
|
0 | ±∞ | F.I. | ±∞ | ±∞ | F.I. |
Remarques :
•
signifie que (V
n) converge vers 0 et que V
n>0 à partir d'un certain rang.
signifie que (V
n) converge vers 0 et que V
n<0 à partir d'un certain rang.
• Lorsque le résultat est ±∞, on applique la règle des signes pour savoir s'il s'agit de +∞ ou de -∞.
• Lorsqu'on arrive à une Forme Indéterminée, cela ne signifie pas forcément que la suite n'a pas de limite. Il faut chercher à lever l'indétermination en transformant l'écriture de la suite.
Exemples :
1) Déterminer
Solution :
•
,
,
.
Par somme,
2) Déterminer
Solution :
•
,
.
Par produit,
•
,
.
Par somme,
3) Déterminer
Solution :
•
,
,
Par différence,
•
,
,
Par somme,
•
,
Par quotient,
Lever une indétermination :
Méthode 1 : Quand le terme général d'une suite est sous forme polynomiale, on peut lever une indétermination en factorisant par le terme de plus haut degré.
Exemple :
Déterminer
Solution :
•
,
, il s'agit d'une Forme Indéterminée.
Factorisons par n
3 :
•
,
.
Par somme,
•
,
,
Par produit,
Méthode 2 : Quand le terme général d'une suite est sous forme rationnelle, on peut lever une indétermination en factorisant le numérateur et leur dénominateur par leur terme de plus haut degré.
Exemple :
Déterminer
Solution :
•
,
, il s'agit d'une Forme Indéterminée.
Factorisons le numérateur par n
2 et le dénominateur par n :
•
,
, par quotient
•
,
, par produit,


Limites et comparaison
Théorème de comparaison :
Soit n
0 un entier naturel. Soit (U
n) et (V
n) deux suites telles que U
n ≤ V
n pour tout n≥n
0.
• Si
, alors
.
• Si
, alors
.
Exemple :
Déterminer
Solution :
≥
, or
, donc
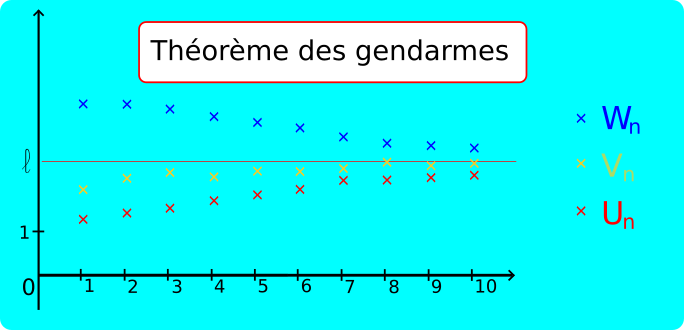
Théorème des gendarmes :
Soit n
0 un entier naturel. Soit (U
n), (V
n) et (W
n) trois suites telles que U
n ≤ V
n ≤ W
n pour tout n≥n
0 et
l un nombre réel.
• Si
l et
l, alors
l.
Exemple :
Déterminer
Solution :
.
Or
.
Donc, d'après le théorème des gendarmes,
Limites des suites monotones
Théorème :
• Une suite
croissante et majorée est
convergente.
• Une suite
décroissante et minorée est
convergente.
• Une suite
croissante non majorée est
divergente vers +∞.
• Une suite
décroissante non minorée est
divergente vers −∞.
Exemple :
Soit (U
n) la suite définie par U
0=9 et U
n+1=
pour tout entier n≥0. Montrer que 1≤U
n+1≤U
n pour tout entier n≥0, en déduire que U
n est convergente.
Solution :
• Soit P(n) = «1≤U
n+1≤U
n»
•
Initialisation : U
0=9 donc U
1=3 et 1≤U
1≤U
0 donc P(0) est vraie.
•
Hérédité : Supposons que P(k) soit vraie pour un certain entier k≥0. On a alors :
1 ≤ Uk+1 ≤ Uk
1 ≤ ≤
1 ≤ ≤
donc P(k+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=0 et est héréditaire, donc par récurrence elle est vraie pour tout n≥0 et 1≤U
n+1≤U
n pour tout n≥0. Donc (U
n) est décroissante et minorée par 1 donc (U
n) est convergente.
Propriétés :
• Si une suite est croissante et converge vers
l, alors elle est majorée par
l.
• Si une suite est décroissante et converge vers
l, alors elle est minorée par
l.
Limite de qn
Propriétés :
Soit
q un nombre réel
• Si
q>1, alors la suite (
qn) diverge vers +∞
• Si
q=1, alors la suite (
qn) converge vers 1
• Si -1<
q<1, alors la suite (
qn) converge vers 0
• Si
q≤-1, alors la suite (
qn) diverge et n'admet pas de limite
Exemples :
1)
car 4>1
2)
car -1<
<1
3)
n'a pas de limite car -3≤-1
Démonstration :
Inégalité de Bernoulli :
Soit a>0. L'inégalité (1 + a)
n ≥ 1 + na est vraie pour tout n∈ℕ
On considère la propriété P(n) = «(1 + a)
n ≥ 1 + na»
•
Initialisation : (1 + a)
0=1 et 1 + 0×a=1 donc P(0) est vraie.
•
Hérédité : Supposons que P(k) soit vraie pour un certain entier k≥0. On a alors :
(1 + a)k ≥ 1 + ka
en multipliant chaque membre de l'inégalité, on obtient:
(1 + a)k+1 ≥ (1 + ka)×(1 + a)
(1 + a)k+1 ≥ 1 + a + ka + ka²
(1 + a)k+1 ≥ 1 + a(k + 1) + ka²
(1 + a)k+1 ≥ 1 + a(k + 1)
donc P(k+1) est vraie et la propriété est héréditaire.
•
Conclusion : la propriété est vraie pour n=0 et est héréditaire, donc par récurrence elle est vraie pour tout n≥0 et (1 + a)
n ≥ 1 + na pour tout n≥0.
Si q>1 : Posons a=
q-1, a>0.
qn=(1+a)
n≥ 1 + na , en utilisant l'inégalité de Bernoulli.
Or
, donc
.
Si 0<q<1 :, donc en utilisant le cas précédent
et par passage à l'inverse,
Si -1<q<0 : quel que soit n ∈ℕ,
≤
≤
,
or
=
=0 . Donc d'après le théorème des gendarmes,
=0