Cours : Fonction exponentielle

La fonction exponentielle

Définition :
Il existe une unique fonction f définie et dérivable sur ℝ telle que f ' = f et f(0) = 1. Cette fonction est appelée fonction exponentielle et se note exp.
• exp(0) = 1
• pour tout x ∈ ℝ , exp'(x) = exp(x)

Relation fonctionnelle

Propriété :
Pour tout réel x et y, on a :

exp(x+y) = exp(x) × exp(y)

Conséquences :
Pour tout réel x et y et pour tout entier relatif n, on a :

•

exp(-x) = \frac{1}{exp(x)}

•

exp(x-y) = \frac{exp(x)}{exp(y)}

•

exp(nx) = {(exp(x))}^{n}

La notation

e^{x}

Définition :
L'image de 1 par la fonction exponentielle est notée e.

exp(1) = e ≈ 2,71828

D'après la propriété précédente, pour tout entier relatif n, exp(n) = exp(n×1) = exp(1)ⁿ = eⁿ.
On peut étendre cette notation à l'ensemble des réels :

exp(x) = e^x

Conséquences :
Pour tout réel x et y et pour tout entier relatif n, on a :

•

e^{x+y} = e^{x} \times e^{y}

•

e^{-x} = \frac{1}{e^{x}}

•

e^{x-y} = \frac{e^{x}}{e^{y}}

•

e^{nx} = {(e^{x})}^{n}

Etude de la fonction exponentielle

Signe de la fonction exponentielle :
La fonction exp est strictement positive sur ℝ.
Démonstration
Quel que soit le nombre réel x, exp(x) = exp(

\frac{x}{2} + \frac{x}{2}

) =

{exp (\frac{x}{2})}^{2}

≥0.
D'autre part exp(x) × exp(-x)=exp(x-x)=exp(0)=1, donc exp(x)≠0
Donc quel que soit le nombre réel x, exp(x)>0

Sens de variation de la fonction exponentielle :
La fonction exp est strictement croissante sur ℝ.
Démonstration
Quel que soit le nombre réel x, exp '(x) = exp(x) > 0, donc exp est strictement croissante sur ℝ.

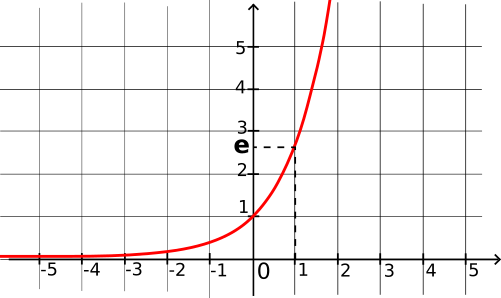Courbe représentative de la fonction exponentielle

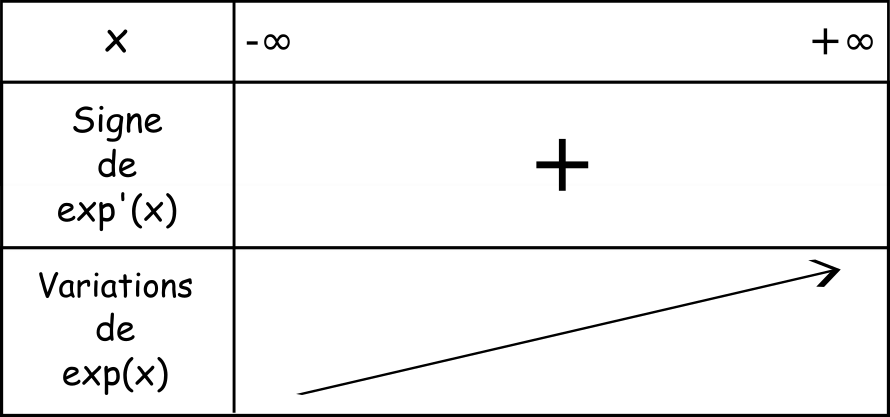Tableau de variations de la fonction exponentielle

Tableau de valeurs (valeurs approchées à 0,001 près):

x	-5	-4	-3	-2	-1	0	1	2	3	4	5
exp(x)	0,007	0,018	0,050	0,135	0,368	1	2,718	7,389	20,086	54,598	148,413

Dérivée de x↦e^u(x) :
Soit u une fonction définie et dérivable sur un intervalle I de ℝ.
La fonction e^u est dérivable sur I et (e^u)'=u' e^u

Représentation graphique des fonctions x↦e^kx et x↦e^-kx :

Soit k un nombre réel strictement positif.
x↦e^kx est strictement croissante et x↦e^-kx est strictement décroissante.

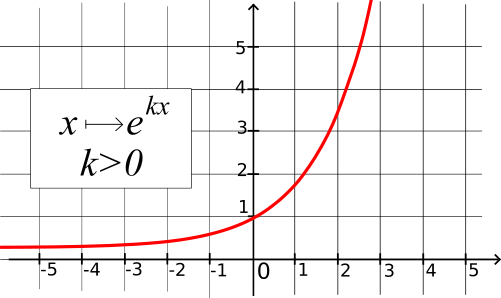courbe représentative de la fonction exp(kx)

Courbe représentative de la fonction x↦e^kx (avec k>0)

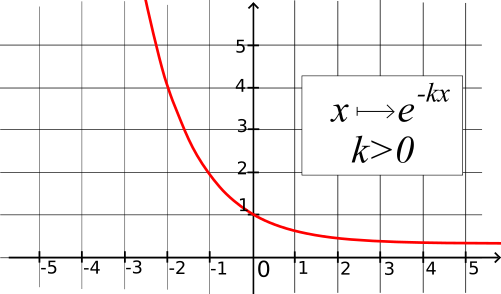Courbe représentative de la fonction x↦e^-kx (avec k>0)

La suite (e^na)

Propriété :

Quel que soit le nombre réel a, la suite (U_n) définie par U_n = e^na pour tout entier naturel n, est une suite géométrique de raison e^a.
Démonstration

\frac{U_{n+1}}{U_{n}} = \frac{e^{(n+1)a}}{e^{na}} = \frac{e^{na+a}}{e^{na}} = \frac{e^{na} e^{a}}{e^{na}} = e^{a}

Exercices :
QCM fonction exponentielle
Propriétés algébriques de la fonction exponentielle
Simplifier une expression avec des exponentielles
Représentation graphique de fonctions exponentielles
Dérivée d'une fonction exponentielle
Dériver une fonction avec des exponentielles