Sens de variations :
Soit
f une fonction définie et dérivable sur un intervalle I.
• Si
f'(x) ≥ 0 pour tout x de I, alors f est
croissante sur I.
• Si
f'(x) ≤ 0 pour tout x de I, alors f est
décroissante sur I.
• Si
f'(x) = 0 pour tout x de I, alors f est
constante sur I.
Exemples :
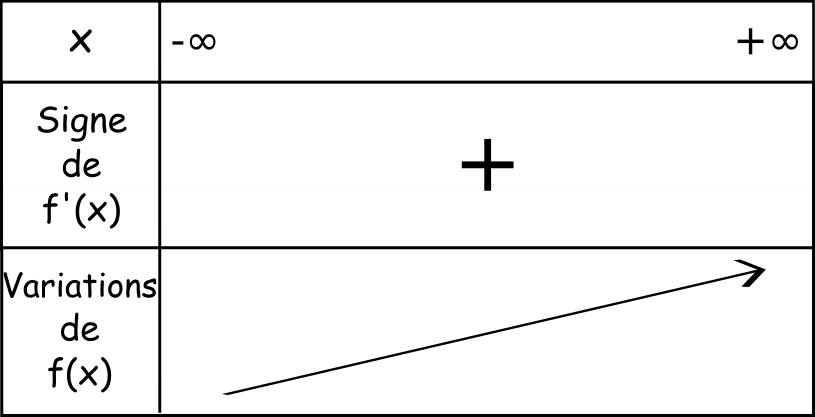
1) Soit
f la fonction définie sur ℝ par
.
f' est positive sur ℝ donc f est croissante sur ℝ.
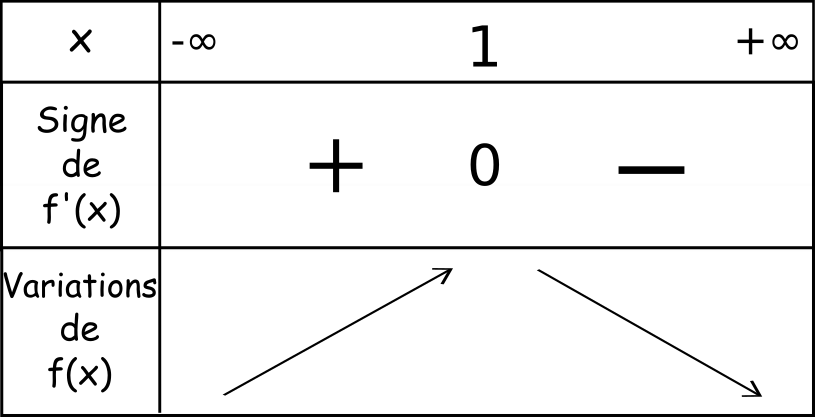
2) Soit
f la fonction définie sur ℝ par
.
est positif sur ]-∞ ; 1[ et négatif sur ]1 ; +∞[ donc f est croissante sur ]-∞ ; 1[ et décroissante sur ]1 ; +∞[.
Extremum local :
Définition :
Soit f une fonction définie et dérivable sur un intervalle I et c un nombre de I.
Dire que f(c) est un
maximum local de f signifie qu'il existe un intervalle ouvert J contenant c et inclus dans I tel que, pour tout x de J,
f(x) ≤ f(c)
Dire que f(c) est un
minimum local de f signifie qu'il existe un intervalle ouvert J contenant c et inclus dans I tel que, pour tout x de J,
f(x) ≥ f(c)
Dire que f(c) est un
extremum local de f signifie que f(c) est un
maximum local ou un
minimum local.
Exemple :
La courbe
Cf ci-dessous représente une fonction f définie sur [-5;5].
Propriété :
Soit f une fonction définie et dérivable sur un intervalle I et c un nombre de I.
Si f admet un
extremum local en c, alors
f'(c)=0.
Exemple :
Soit
f la fonction définie sur ℝ par
.
est négatif sur ]-∞ ; -2[ et positif sur ]-2 ; +∞[.
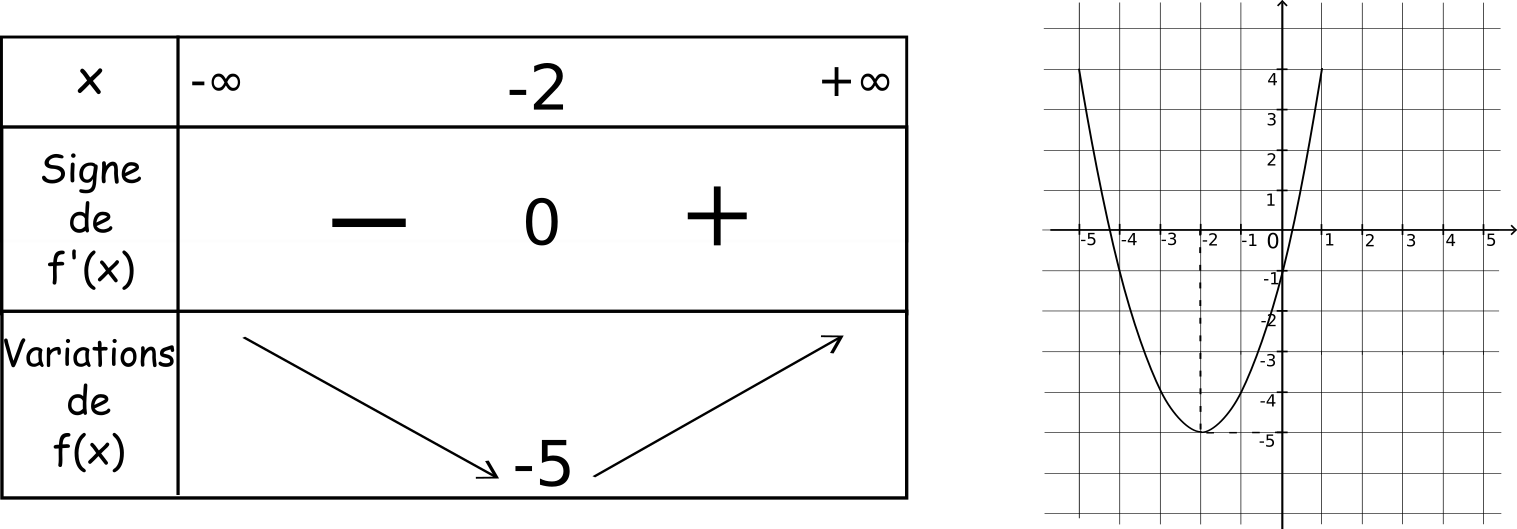
f(-2) = -5 est un extremum local de f donc f'(-2)=0.
/!\ la réciproque est fausse.
Exemple : Soit f définie par f(x) = x³. f'(x) = 3x² donc f'(0)=0 or f n'admet pas d'extremum local en 0.


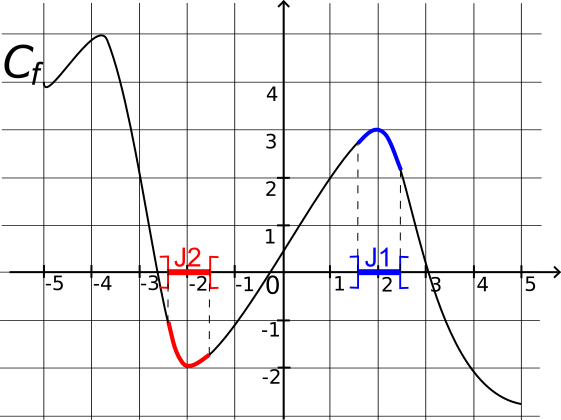



Pour tout x de l'intervalle J1, f(x) ≤ f(2) donc f(2)=3 est un maximum local de f.
Pour tout x de l'intervalle J2, f(x) ≥ f(-2) donc f(-2)=-2 est un minimum local de f.