Cours : Variables aléatoires

Définition : Soit E l'ensemble des issues d'une expérience aléatoire. Définir une variable aléatoire X sur E, c'est associer à chaque issue de E un nombre x.

Exemple :
Une urne contient 2 boules bleues, une boule rouge et une boule verte. Un jeu consiste à tirer une boule de cette urne. On gagne 8€ si la boule est verte ,on gagne 4€ si la boule est bleue mais on perd 20€ si la boule est rouge. On peut définir une variable aléatoire X sur E qui prend les valeurs -20; 4 et 8.

• L'événement (X=8) est réalisé lorsque la boule tirée est verte.

• L'événement (X=4) est réalisé lorsque la boule tirée est bleue.

• L'événement (X=-20) est réalisé lorsque la boule tirée est rouge.

Loi de probabilité :
Soit X une variable aléatoire sur un univers E. On note x_i les différentes valeurs prises par X.
Lorsqu'on associe à chaque valeur x_i, la probabilité de l'évènement (X = x_i), on définit une loi de probabilité.

Exemple :
On reprend l'exemple précédent. La probabilité de l'événement (X = -20) est la probabilité de tirer la boule rouge, c'est à dire P(X = -20) =

\frac{1}{4}

.
La probabilité de l'événement (X = 4) est la probabilité de tirer une boule bleue, c'est à dire P(X = 4) =

\frac{1}{2}

.
La probabilité de l'événement (X = 8) est la probabilité de tirer une boule verte, c'est à dire P(X = 8) =

\frac{1}{4}

.

On peut résumer la loi de probabilité dans un tableau :

x_i	-20	4	8
P(X = x_i)	$\frac{1}{4}$	$\frac{1}{2}$	$\frac{1}{4}$

Paramètres d'une variable aléatoire : On considère une variable aléatoire X définie sur E dont la loi de probabilité est résumée ci-dessous :

Valeur de X	x₁	x₂	...	x_n
P(X = x_i)	p₁	p₂	...	p_n

• L'espérance de la variable aléatoire X est le nombre réel, noté E(X), défini par :

E(X) = p_{1} x_{1} + p_{2} x_{2} + ... + p_{n} x_{n}

• La variance de la variable aléatoire X est le nombre réel, noté V(X), défini par :

V(X) = p_{1} {(x_{1} - E(X))}^{2} + p_{2} {(x_{2} - E(X))}^{2} + ... + p_{n} {(x_{n} - E(X))}^{2}

• L'écart-type de la variable aléatoire X est le nombre réel, noté σ(X), défini par :

σ(X) = \sqrt{V(X)}

Exemple :
On reprend l'exemple précédent :

x_i	-20	4	8
P(X = x_i)	$\frac{1}{4}$	$\frac{1}{2}$	$\frac{1}{4}$

•

E(X) = \frac{1}{4} \times 20 + \frac{1}{2} \times 4 + \frac{1}{4} \times 8 = -5 + 2 + 2 = -1

•

V(X) = \frac{1}{4} \times {(-20 - (-1))}^{2} + \frac{1}{2} \times {(4 - (-1))}^{2} + \frac{1}{4} \times {(8 - (-1))}^{2}

V(X) = \frac{1}{4} \times {(-19)}^{2} + \frac{1}{2} \times {(5)}^{2} + \frac{1}{4} \times {(9)}^{2}

V(X) = \frac{1}{4} \times 361 + \frac{1}{2} \times 25 + \frac{1}{4} \times 81

V(X) = 90,25 + 12,5 + 20,25 = 123

• σ(X) =

\sqrt{123}

≈ 11,09

Utilisation de la calculatrice :
-> Avec le mode stat des modèles Casio :

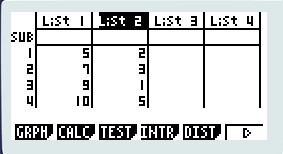
1) Choisir le menu stat et compléter les deux premières colonnes list1 et list2 par les valeurs de la série moyenne avec casio

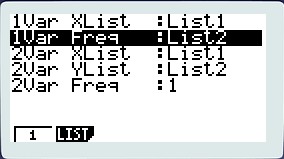
2) Choisir calc (f2) puis Set (f6) puis choisir List1 pour la ligne 1Var Xlist et List2 pour la ligne 1Var Freq ecart type avec casio

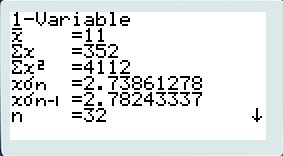
3) Taper exit puis 1var (f1), lire les valeurs de la moyenne et de l'écart-type (xσn) ici : 2.73861278 variance avec casio

-> Avec la touche Stat des modèles TI :

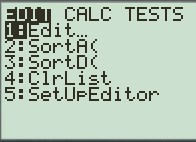
1) Taper la touche Stat puis edit (1) moyenne avec ti

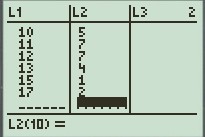
2) Compléter les deux premières colonnes (L1 et L2) variance avec ti

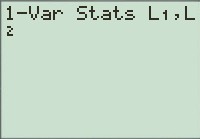
3) Taper Stat puis choisir calc puis 1-Var stats L1,L2 ecart-type avec ti

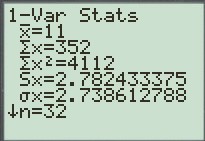
4) Il suffit alors lire les valeurs de la moyenne et de l'ecart-type (noté σx) ici : 2.738612788 ecart-type avec ti

Remarque : La calculatrice ne fournit pas la valeur de la variance, pour la retrouver, il suffit d'élever la valeur de l'écart-type au carré.