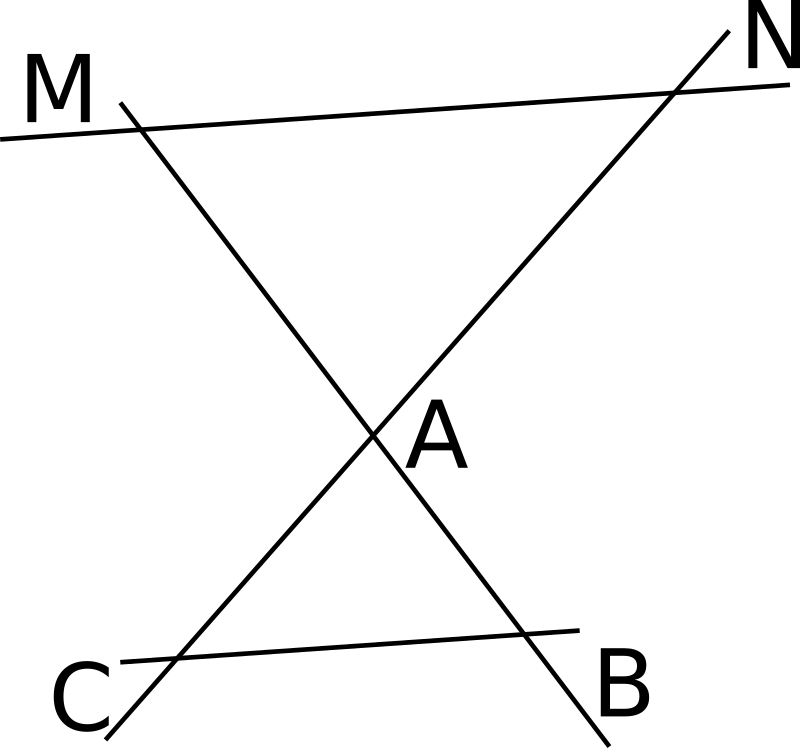
Théorème de Thalès : Soient (BM) et (CN) deux droites sécantes en A. Si les droites (BC) et (MN) sont parallèles, alors :

Configurations de Thalès :
Les 3 figures suivantes sont représentent des situations de Thalès où les droites (BC) et (MN) sont parallèles.

On sait que : • les droites (BM) et (CN) sont sécantes en A. • Les droites (MN) et (BC) sont parallèles.

On en déduit que : $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{\mathrm{MN}}{\mathrm{BC}}$

Application 1 : Calculer la longueur d'un segment.

Énoncé : Calculer la longueur du segment [IP] sachant que KI = 2,2 cm, JI = 3 cm, IQ = 4,5 cm et que les droites (JK) et (PQ) sont parallèles.

Solution : Les droites (KP) et (JQ) sont sécantes en I et les droites (JK) et (PQ) sont parallèles. D'après le théorème de Thalès, on a: $\frac{\mathrm{IK}}{\mathrm{IP}}=\frac{\mathrm{IJ}}{\mathrm{IQ}}=\frac{\mathrm{KJ}}{\mathrm{QP}}$ donc $\frac{\mathrm{2,2}}{\mathrm{IP}}=\frac{3}{\mathrm{4,5}}$ donc $\mathrm{IP}=\frac{\mathrm{2,2}\times \mathrm{4,5}}{3}=\mathrm{3,3}$ donc IP = 3,3 cm.

Application 2 : Montrer que deux droites ne sont pas parallèles.

Énoncé : Montrer que les droites (BC) et (MN) ne sont pas parallèles.

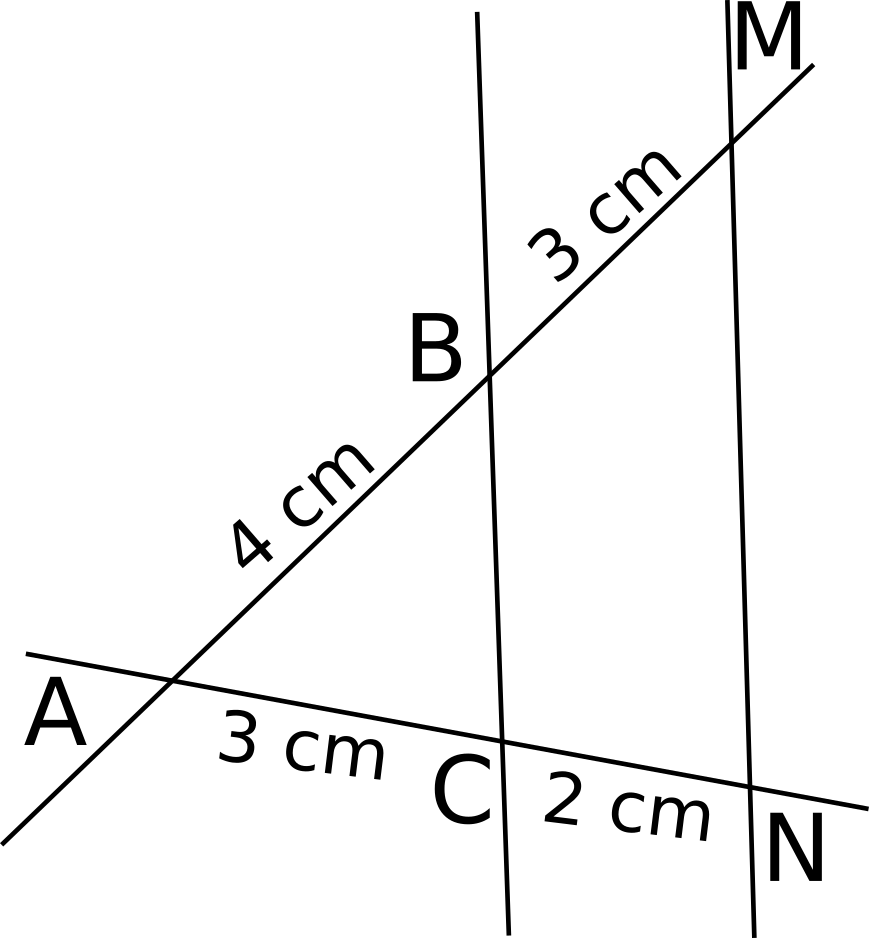
Solution : Les droites (BM) et (CN) sont sécantes en A. D'une part : $\frac{\mathrm{AC}}{\mathrm{AN}}=\frac{3}{5}=\mathrm{0,6}$ D'autre part : $\frac{\mathrm{AB}}{\mathrm{AM}}=\frac{4}{7}\approx \mathrm{0,57}$ donc $\frac{\mathrm{AC}}{\mathrm{AN}}\ne \frac{\mathrm{AB}}{\mathrm{AM}}$ donc les droites (BC) et (MN) ne sont pas parallèles, sinon les rapports précédents seraient égaux d'après le théorème de Thalès.

Réciproque du théorème de Thalès : Soient (BM) et (CN) deux droites sécantes en A.
Si :
• $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$
• les points A, M, B et les points A, N, C sont alignés dans le même ordre.
Alors :
les droites (MN) et (BC) sont parallèles.

Exemple :

On sait que : • les droites (BM) et (CN) sont sécantes en A. • $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$ • Les points M, A, B et N, A, C sont alignés dans cet ordre.

On en déduit que : Les droites (MN) et (BC) sont parallèles

Application :
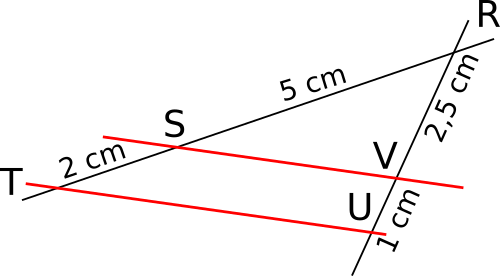
Montrer que les droites (SV) et (TU) sont parallèles.

• Les droites (TS) et (UV) sont sécantes en R. • D'une part $\frac{\mathrm{RT}}{\mathrm{RS}}=\frac{7}{5}=\mathrm{1,4}$ , d'autre part $\frac{\mathrm{RU}}{\mathrm{RV}}=\frac{\mathrm{3,5}}{\mathrm{2,5}}=\mathrm{1,4}$ , donc $\frac{\mathrm{RU}}{\mathrm{RV}}=\frac{\mathrm{RT}}{\mathrm{RS}}$ • De plus, les points R, S, T et R, V, U sont alignés dans cet ordre. Donc d'après la réciproque du théorème de Thalès, les droites (SV) et (TU) sont parallèles.

Exercices :
Rédiger le théorème de Thalès
Appliquer le théorème de Thalès
Réciproque du théorème de Thalès

Fiche précédente :
Trigonométrie Fiche suivante :
Angles inscrits - Polygones réguliers