Cours : Suites arithmétiques

Définition :

Dire qu'une suite u est arithmétique signifie qu'il existe un nombre r tel que, pour tout entier naturel n, u_n+1 = u_n + r. Le nombre r est appelé la raison de la suite (u_n).

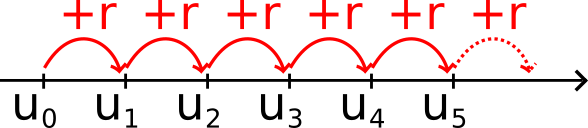
Autrement dit, on passe d'un terme d'une suite arithmétique au terme suivant en ajoutant toujours le même nombre r.

Exemples :
1) Soit u la suite des entiers naturels 0, 1, 2, 3, 4, 5, ... u est la suite arithmétique de premier terme 0 et de raison 1
2) Soit v la suite des multiples de 3 : 0, 3, 6, 9, 12 ... v est la suite arithmétique de premier terme 0 et de raison 3
3) Soit w la suite définie pour tout entier naturel n par w_n = 4n + 7.
w_n+1 - w_n = 4(n+1) + 7 - (4n + 7) = 4n + 4 - 7 - 4n - 7 = 4
Donc w_n+1 - w_n = 4 d'où w_n+1 = w_n + 4.
De plus w₀ = 7, donc w est la suite arithmétique de premier terme 7 et de raison 4.

Formule explicite :

Pour calculer un terme d'une suite arithmétique avec la définition par récurrence, il est nécessaire de connaître le terme précédent. La propriété suivante permet de trouver une formule explicite.
Si u est une suite arithmétique de raison r, alors, pour tout entier naturel n et p :

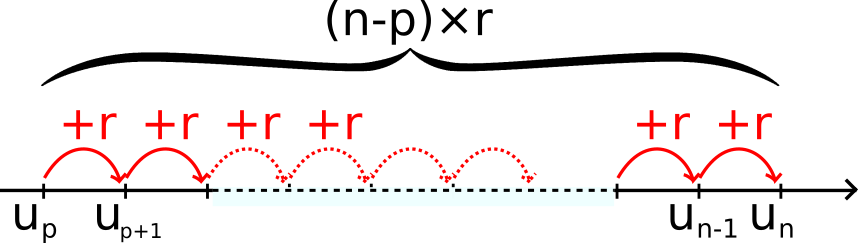
u_n = u_p + (n-p)r

Illustration :

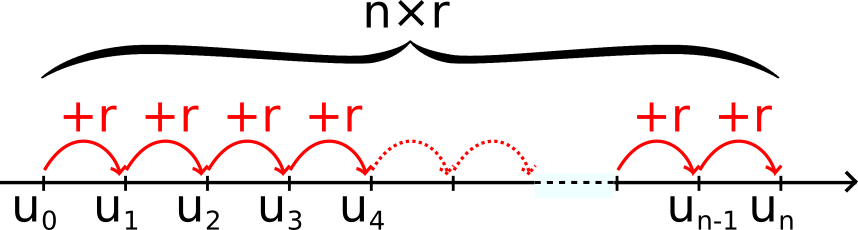
En particulier, si p = 0, pour tout entier naturel n, on a :

u_n = u₀ + nr

Illustration :

cas particulier formule suites arithmétiques

Exemples :
1) Soit u la suite arithmétique de raison r=7 et de premier terme u₀=5. Calculer u₁₂.

Réponse :

D'après la deuxième formule, u₁₂ = u₀ + 12 × r = 5 + 12 × 7 = 5 + 84 = 89.

2) Soit v la suite arithmétique de raison r=3 telle que u₅=49. Calculer u₂₁.

Réponse :

D'après la première formule, u₂₁ = u₅ + (21 - 5) × r = 49 + 16 × 3 = 49 + 48 = 97.

Somme des termes d'une suite arithmétique :

I) Somme des entiers de 1 à n :
Pour tout entier naturel n non nul, on a :

1 + 2 + 3 + ... + n = \frac{n(n + 1)}{2}

Démonstration :
On appelle S la somme des entiers de 1 à n. On écrit sur une ligne la somme des termes dans l'ordre croissant, de 1 à n, puis sur une seconde ligne, on écrit cette somme dans l'ordre décroissant de n à 1 et on additionne membre à membre les deux égalités.

...+

n-1

n-2

...+

(n+1)

...+

(n+1)

2S est donc égal à la somme de n termes tous égaux à (n+1) d'où 2S = n(n+1) soit

S = \frac{n(n + 1)}{2}

Exemple :

S = 1 + 2 + 3 + ... + 50

S = \frac{50(50 + 1)}{2}

S = 25 × 51

= 1275

II) Somme des termes d'une suite arithmétique :
Soit u une suite arithmétique. La somme des n premiers termes d'une suite arithmétique est égale à :

S = nombre de termes × \frac{premier terme + dernier terme}{2}

Remarques :
• Si on note u₀ le premier terme :
S = u₀ + u₁+ ... + u_n est égale à la somme des (n + 1) premiers termes de la suite et:

S = (n+1) × \frac{u_{0} + u_{n}}{2}

• Si on note u₁ le premier terme :
S = u₁ + u₂ + ... + u_n est égale à la somme des n premiers termes de la suite et:

S = n × \frac{u_{1} + u_{n}}{2}

Exemple :
Soit u la suite arithmétique de premier terme u₀ = 1 et de raison 4.
Calculer la somme S = u₀ + u₁ + u₂ + ... + u₁₂.

Réponse :

La formule explicite de u est u_n = 4n + 1, donc u₁₂ = 4 × 12 + 1 = 48 + 1 = 49.
Donc :

S = (12+1) × \frac{u_{0} + u_{12}}{2}

S = 13 × \frac{1 + 49}{2}

S = 13 × 25 = 325