Conditionnement par un évènement
Définition :
Soient A et B deux évènements de Ω tels que P(B)≠0.
La probabilité que l'évènement A soit réalisé sachant que B est réalisé (on dira simplement probabilité de A sachant B) est notée
.
La probabilité de A sachant B est définie par :
Exemple :
Une société comprend 25% de cadres. De plus 10% de la totalité des employés sont des hommes et sont cadres . On interroge au hasard un employé de cette entreprise.
Quelle est la probabilité que l'employé interrogé soit un homme sachant que c'est un cadre ?
On note C l'évènement «l'employé interrogé est un cadre» et H l'évènement «l'employé interrogé est un homme».
D'après l'énoncé, on a P(C) = 0,25 et P(C∩H) = 0,1.
Donc la probabilité que l'employé interrogé soit un homme sachant que c'est un cadre est égale à 0,4.
Conséquence :
Soient A et B deux évènements de Ω tels que P(B)≠0.
Exemple :
Lors d'un sondage, 80% des personnes interrogées parlent anglais, et parmi elles, 30% parlent espagnol.
On choisit au hasard une personne interrogée lors de ce sondage, quelle est la probabilité que cette personne parle anglais et espagnol ?
On note A l'évènement «la personne interrogée parle anglais» et E l'évènement «la personne interrogée parle espagnol».
D'après l'énoncé, on a P(A) = 0,8 et
0,3
= 0,8 × 0,3 = 0,24
Donc la probabilité que la personne interrogée parle anglais et espagnol est égale à 0,24.
Arbre pondéré
Cas général :
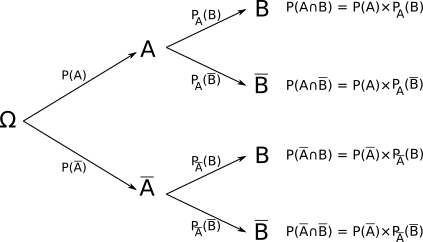
On peut représenter une expérience faisant intervenir des probabilités conditionnelles par un arbre pondéré.
• Règle 1 : Sur les branches issues de Ω, on inscrit les probabilités des évènements correspondants
• Règle 2 : Sur les branches suivantes, on inscrit les probabilités conditionnelles
• Règle 3 : La somme des probabilités inscrites sur les branches d'un même noeud est égale à 1
• Règle 4 : Une succession de plusieurs branches est appelé un chemin. Un chemin représente l'intersection des évènements rencontrés, sa probabilité est égale au produit des probabilités notées sur ses branches.
Exemple :
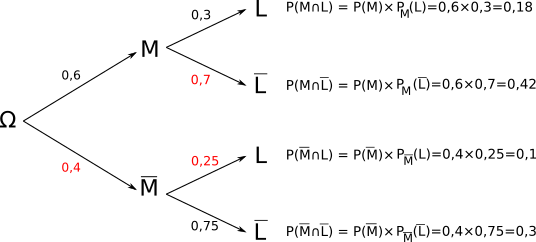
Dans une certaine population, 60% des individus ont les yeux marron. Parmi les individus qui ont les yeux marron, 30% portent des lunettes. Parmi les individus qui n'ont pas les yeux marron, 75% ne portent pas de lunettes.
• Soit M l'évènement «l'individu a les yeux marron»
• Soit M l'évènement «l'individu n'a pas les yeux marron»
• Soit L l'évènement «l'individu porte des lunettes»
• Soit L l'évènement «l'individu ne porte pas de lunettes»
Partition de l'univers
Définition :
Les évènements A
1, ... ,A
n (avec n entier supérieur ou égal à 2) forment une partition de l'univers Ω lorsque:
• pour tout entier i tel que 1≤i≤n , A
i ≠ 0.
• pour tous entiers i et j tel que 1≤i≤n et 1≤j≤n et i ≠ j , A
i ∩ A
j = Ø.
• A
1 ∪...∪ A
n = Ω
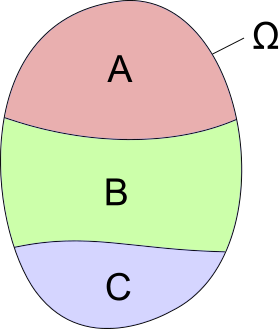
Sur l'illustration ci-contre, les évènements A, B et C forment une partition de l'univers Ω.
A∩B = Ø, A∩C = Ø, B∩C = Ø et A∪B∪C = Ω.
Exemple :
On tire une carte dans un jeu de 32 cartes. On note R l'évènement «la carte est rouge», P l'évènement «la carte est un pique» et T l'évènement «la carte est un trèfle».
Les évènements R, P et T forment une partition de l'univers.
Cas particulier :
Quel que soit l'évènement A de probabilité non nulle et inférieure à 1, les évènements A et A forment une partition de l'univers.
Formule des probabilités totales :
• Cas général :
Si B
1, ... ,B
n (avec n entier supérieur ou égal à 2) forment une partition de l'univers Ω , alors :
ou
• Cas particulier :
Si B est un évènement de probabilité non nulle et inférieure à 1, alors pour tout évènement A, on a :
ou
Exemple :
On s'intéresse à la LV2 choisie par les élèves d'un certain lycée.
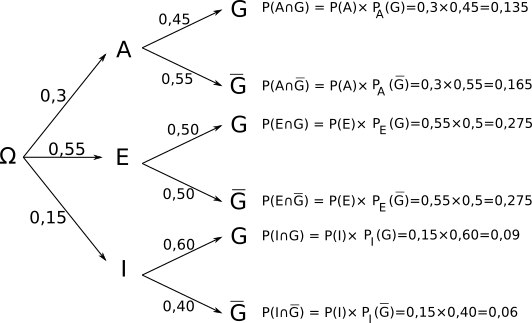
• 30% des élèves ont choisi allemand (A), dont 45% de garçon (G).
• 55% des élèves ont choisi espagnol (E), dont 50% de garçon (G).
• 15% des élèves ont choisi italien (I), dont 60% de garçon (G).
On choisit au hasard un élève de ce lycée.
Quelle est la probabilité que cet élève soit un garçon?
Réponse: Les évènements A, E et I forment une partition de l'univers.
D'après la formule des probabilités totales, on a:
La probabilité que l'élève soit un garçon est égale à 0,5.
Indépendance
Définition :
On dit que deux évènements A et B sont
indépendants si :
P(A∩B) = P(A)×P(B)
Propriétés :
Si deux évènements A et B sont
indépendants, alors
A et B sont indépendants.
Propriétés :
Soient A et B deux évènements de probabilités non nulles.
• A et B sont
indépendants si et seulement si
(autrement dit, la probabilité de B n'est pas influencée par la réalisation ou non de A)
• A et B sont
indépendants si et seulement si
(autrement dit, la probabilité de A n'est pas influencée par la réalisation ou non de B)
Exemple :
On tire une carte dans un jeu de 32 cartes. On note C l'évènement «la carte tirée est un coeur» et D l'évènement «la carte tirée est une dame».
P(C) = 8/32 = 1/4 et P(D) = 4/32 = 1/8, d'où P(C)×P(D) = 1/32.
L'évènement C∩D n'a qu'une issue ( la dame de coeur), donc P(C∩D) = 1/32.
D'où P(C∩D)= P(C)×P(D), donc les évènements C et D sont indépendants.