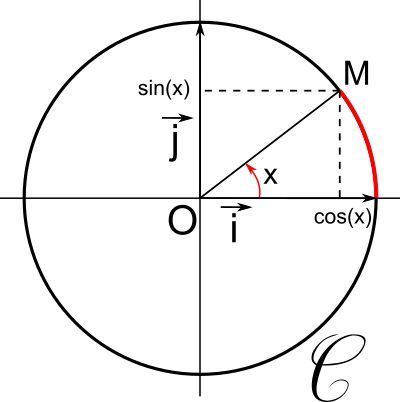
Soit (O;
,
) un repère orthonormé et
le cercle trigonométrique de centre O.
Soit
x un nombre réel et M l'image de
x sur le cercle
Le
cosinus de
x, noté
cos(x) est l'abscisse de M.
Le
sinus de
x, noté
sin(x) est l'ordonnée de M.
Définitions :
• La fonction x↦sin x définie sur ℝ est appelée fonction sinus et notée sin.
• La fonction x↦cos x définie sur ℝ est appelée fonction cosinus et notée cos.
Dérivabilité
Propriété :
Les fonctions sinus et cosinus sont
continues et
dérivables sur ℝ et pour tout réel x :
• sin'(x) = cos(x)
• cos'(x) = -sin(x)
Exemples :
1) Soit f la fonction définie sur ℝ par f(x) = x + cos(x) , f est dérivable sur ℝ et f'(x) = 1 - sin(x)
2) Soit g la fonction définie sur ℝ par g(x) = 2sin(x) - cos(x) , g est dérivable sur ℝ et g'(x) = 2cos(x) + sin(x)
Propriété :
Soit u une fonction dérivable sur un intervalle I de ℝ.
• La fonction cos(u) est dérivable sur I et cos'(u) = -u'×sin(u)
• La fonction sin(u) est dérivable sur I et sin'(u) = u'×cos(u)
• sin'(u) = u' × cos(u)
• cos'(u) = -u' × sin(u)
Exemples :
1) Soit f la fonction définie sur ℝ par f(x) = cos(3x+4) , f est dérivable sur ℝ et f'(x) = -3sin(3x+4)
2) Soit g la fonction définie sur ℝ par g(x) = sin(x²) , g est dérivable sur ℝ et g'(x) = 2xcos(x²)
Variations des fonctions sinus et cosinus
Propriétés :
Parité - Quel que soit le réel x :
•
sin(-x) = -sin(x) donc la fonction sinus est
impaire.
•
cos(-x) = cos(x) donc la fonction cosinus est
paire.
Périodicité - Quel que soit le réel x :
sin(x+2π) = sin(x) et
cos(x+2π) = cos(x) donc les fonctions sinus et cosinus sont
périodiques de période 2π (ou 2π-périodiques).
Tableaux de variations :
![tableau de variations de sinus sur [-π;π]](./images/varsin.png)
Tableau de variations de la fonction sinus sur [-π;π]
![tableau de variations de cosinus sur [-π;π]](./images/varcos.png)
Tableau de variations de la fonction cosinus sur [-π;π]
Représentations graphiques :
Les courbes représentatives des fonctions sinus et cosinus sont appelées des
sinusoïdes.
![Représentation graphique de la fonction sinus sur [-2π;2π]](./images/foncsin.png)
Représentation graphique de la fonction sinus sur [-2π;2π]
![Représentation graphique de la fonction cosinus sur [-2π;2π]](./images/fonctcos.png)
Représentation graphique de la fonction cosinus sur [-2π;2π]
Equations et inéquations sur [-π;π] :
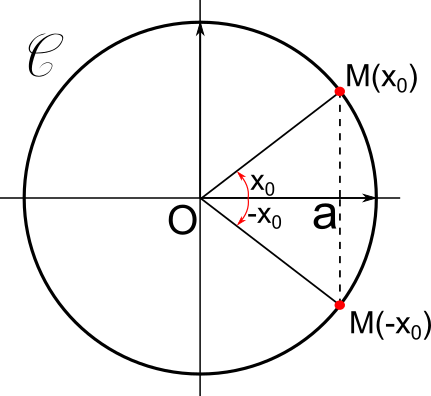
cos(x) = a
Soit a un nombre réel.
On note S l'ensemble solution de l'équation cos(x) = a sur [-π;π].
• Si a<-1, alors S = ∅
• Si a=-1, alors S = {-π;π}
• Si -1 < a < 1, alors S = {-x0;x0} avec x0 tel que cos(x0) = a et x0∈]0;π[
• Si a=1, alors S = {0}
• Si a>1, alors S = ∅
Exemples :
1) Résoudre l'équation cos(x) =
sur [-π;π]
L'équation admet 2 solutions :
et
2) Résoudre l'équation cos(x) = 0,2 sur [-π;π]
L'équation admet 2 solutions : x
0 et x
1 avec x
0≈ 1,37 (on trouve cette valeur avec la touche cos
-1 de la calculatrice) et x
1=-x
0 ≈ -1,37.
3) Résoudre l'équation cos(x) = 2 sur [-π;π]
L'équation n'admet pas de solution.
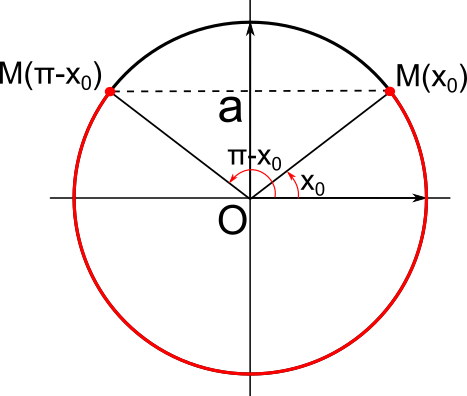
cos(x) ≤ a
Soit a un nombre réel.
On note S l'ensemble solution de l'inéquation cos(x) ≤ a sur [-π;π].
• Si a < -1, alors S = ∅
• Si a=-1, alors S = {-π;π}
• Si -1 < a < 1, alors S = [-π;-x0]∪[x0;π] avec x0 tel que cos(x0) = a et x0∈]0;π[
• Si a≥1, alors S = [-π;π]
Exemple :
Soit S l'ensemble solution de l'inéquation cos(x) ≤
sur [-π;π].
cos(
) =
donc S=[-π;
]∪[
;π]
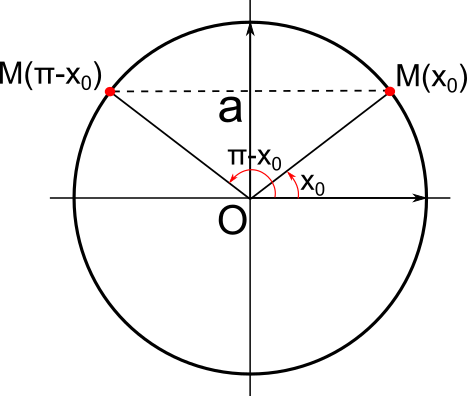
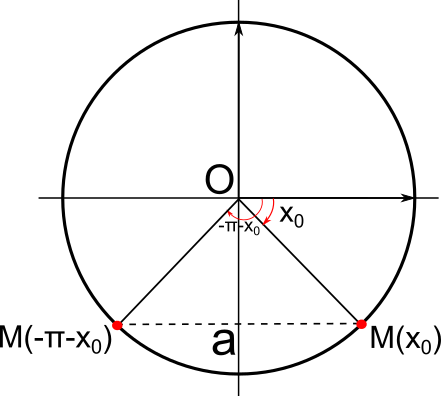
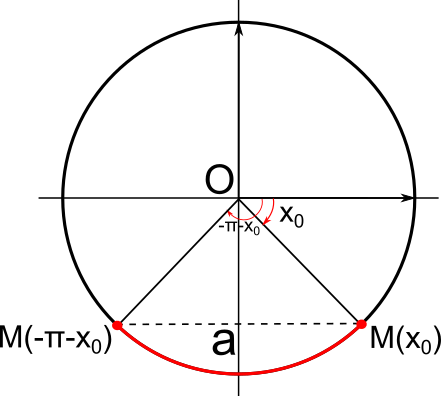
sin(x) = a
Soit a un nombre réel.
On note S l'ensemble solution de l'équation sin(x) = a sur [-π;π].
• Si a < -1, alors S = ∅
• Si a=-1, alors S = {}
• Si -1 < a < 0, alors S = {-π-x0;x0} avec x0 tel que sin(x0) = a et x0∈]-π;0[
• Si a=0, alors S = {-π;0;π}
• Si 0 < a < 1, alors S = {π-x0;x0} avec x0 tel que sin(x0) = a et x0∈]0;π[
• Si a=1, alors S = {}
• Si a>1, alors S = ∅
Exemples :
1) Résoudre l'équation sin(x) =
sur [-π;π]
L'équation admet 2 solutions :
et
2) Résoudre l'équation sin(x) = 0,8 sur [-π;π]
L'équation admet 2 solutions : x
0 et x
1 avec x
0≈ 0,93 (on trouve cette valeur avec la touche sin
-1 de la calculatrice) et x
1=π-x
0 ≈ 2,21.
3) Résoudre l'équation sin(x) = -2 sur [-π;π]
L'équation n'admet pas de solution.
sin(x) ≤ a
Soit a un nombre réel.
On note S l'ensemble solution de l'équation sin(x) ≤ a sur [-π;π].
• Si a < -1, alors S = ∅
• Si a=-1, alors S = {}
• Si -1 < a < 0, alors S = [-π-x0;x0] avec x0 tel que sin(x0) = a et x0∈]-π;0[
• Si a=0, alors S = [-π;0]∪{π}
• Si 0 < a < 1, alors S = [-π;x0]∪[π-x0;π] avec x0 tel que sin(x0) = a et x0∈]0;π[
• Si a≥1, alors S = [-π;π]
Exemples :
Soit S l'ensemble solution de l'inéquation sin(x) ≤
sur [-π;π]
sin(
) =
, donc S = [-π;
]∪[
;π]
