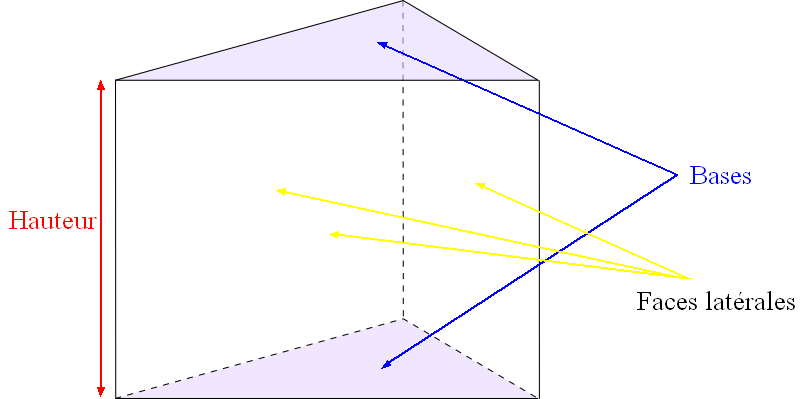
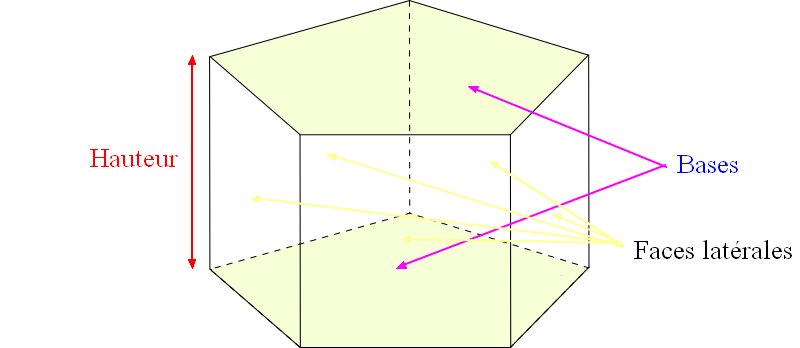
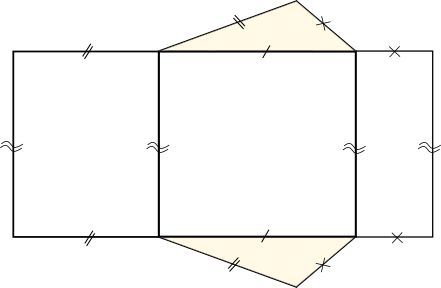
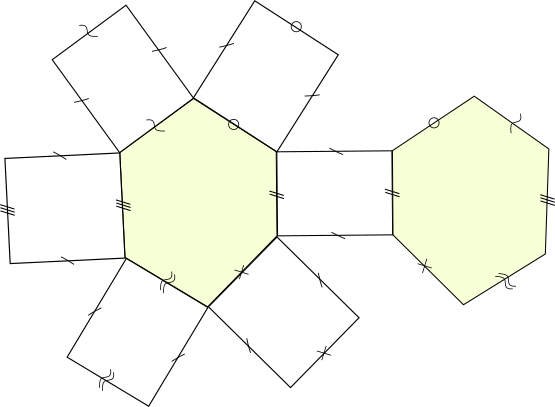
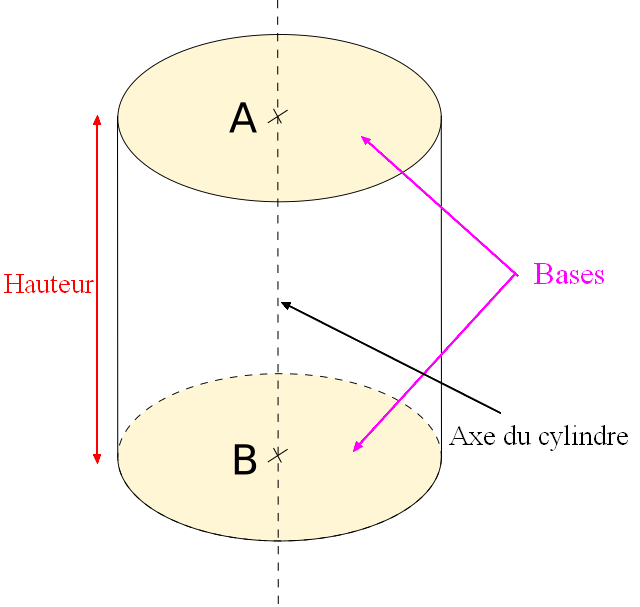
Cas particulier : Un
prisme droit dont la base est un rectangle est un
parallélépipède rectangle.
Aire latérale d'un prisme droit :
La
surface latérale d'un prisme droit correspond à l'ensemble des faces latérales.
L'
aire latérale d'un prisme droit est égale à l'aire de sa surface latérale.
Aire latérale = Périmètre d'une base × hauteur
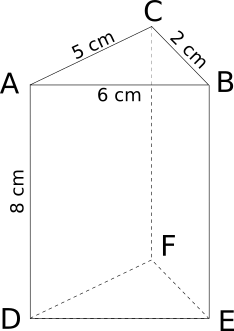
Exemple :
Périmètre d'une base = 6 + 5 + 2 = 13 cm
vertical-align:top;Hauteur = 8 cm
vertical-align:top;
Aire latérale = 13 × 8 = 104 cm
Volume d'un prisme droit :
Le
volume d'un prisme droit est égal au produit de l'aire d'une base par la hauteur.
vertical-align:top;
Volume = Aire d'une base × hauteur
Exemple :
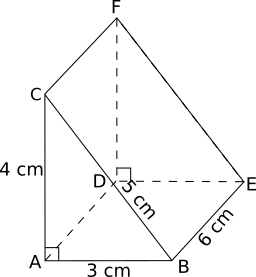
Les bases du prisme ABCDEF sont les triangles rectangles ABC et DEF.
Calculons l'
aire du triangle ABC :
AABC=
=6 cm²
La hauteur du prisme est égale à 6 cm.
Soit
V le volume du prisme :
V = 6 × 6 = 36 cm³
Exemple :
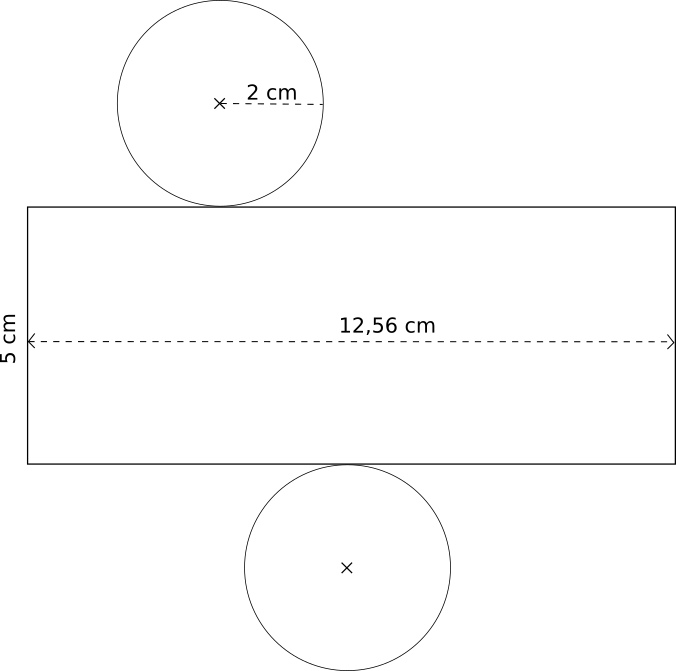Patron d'un cylindre de révolution de rayon 2cm et de hauteur 5cm
Pour déterminer la longueur du rectangle de la surface latérale, il faut calculer le
périmètre d'un cercle de rayon 2cm :
P = 2×
π×R = 2×
π×2 = 4×
π ≈ 12,56 cm.
La largeur est égale à la hauteur du cylindre soit 5cm.
Aire latérale d'un cylindre de révolution :
L'
aire latérale d'un cylindre de révolution est égale à l'aire de sa surface latérale.
Aire latérale = Périmètre d'une base × hauteur
Exemple :
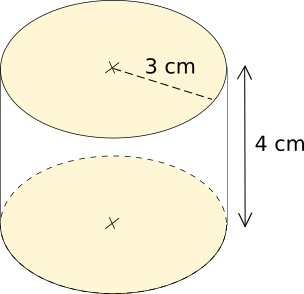
Quelle est l'aire latérale d'un cylindre de révolution de rayon 3 cm et de hauteur 4 cm ?
Périmètre d'une base = 2×π×R = 2×π×3 = 6×π ≈ 18,8 cm.
Hauteur = 4 cm
Aire latérale ≈ 18,8 × 4
Aire latérale ≈ 75,2 cm²
Volume d'un cylindre de révolution :
Le
volume d'un cylindre de révolution est égal au produit de l'aire d'une base par la hauteur.
Volume = Aire d'une base × hauteur
Exemple :
Les bases sont des disques de rayon 6 cm.
Calculons l'
aire d'un disque de rayon 6 cm :
A =
π × R² =
π × 6² = 36 ×
π ≈ 113 cm².
La hauteur du cylindre est égale à 5 cm.
Soit
V le volume du cylindre :
V ≈ 113 × 5
V ≈ 565 cm³
