Définition :
Un parallélogramme est un quadrilatère qui a les côtés opposés parallèles.
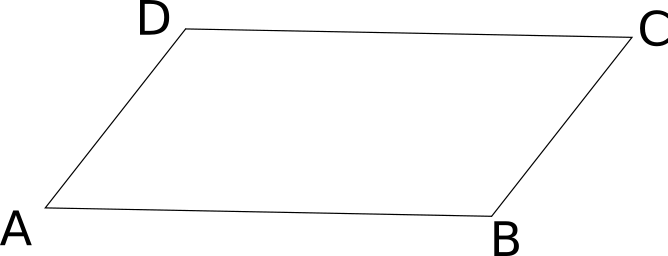
Exemple :

Propriétés :
Si un quadrilatère est un parallélogramme, alors :
• ses diagonales se coupent en leur milieu
• ses côtés opposés sont de même longueur
• ses angles opposés sont de même mesure
• le point d'intersection de ses diagonales est le centre de symétrie de ce quadrilatère.

Exemple :

Reconnaître un parallélogramme :
• Si un quadrilatère a ses côtés opposés parallèles deux à deux , alors c'est un parallélogramme
• Si un quadrilatère a ses diagonales qui se coupent en leur milieu , alors c'est un parallélogramme
• Si un quadrilatère non croisé a ses côtés opposés de même longueur deux à deux, alors c'est un parallélogramme
• Si un quadrilatère non croisé a deux côtés parallèles et de même longueur, alors c'est un parallélogramme.