Propriété :
La somme des mesures des angles d'un triangle est égale à
180°.
Exemple :
Dans le triange ABC ci-dessous, on a :
+
+
= 79° + 58° + 43° = 180°.
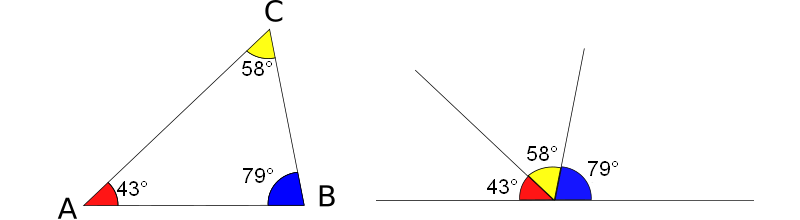En plaçant les trois angles l'un à côté de l'autre, on obtient un angle plat.
Somme des angles d'un triangle rectangle :
Dans un triangle rectangle, la somme des mesures des
angles aigus est égale à
90°.
Exemple :
Dans le triange ABC rectangle en B ci-dessous, on a :
+
= 55° + 35° = 90°.
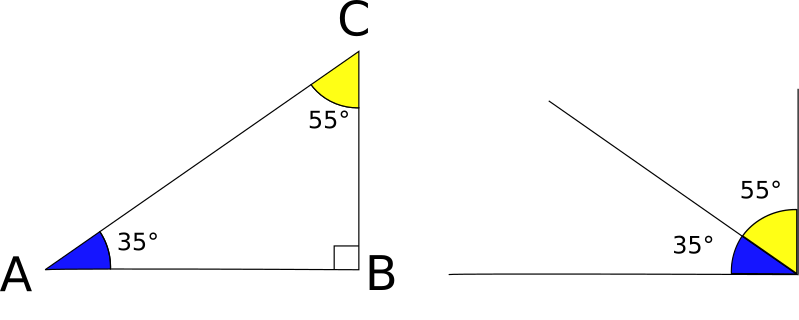En plaçant les deux angles aigus l'un à côté de l'autre, on obtient un angle droit.
Somme des angles d'un triangle isocèle :
Dans un triangle isocèle, les angles à la base sont de même mesure, on peut donc retrouver la mesure de tous les angles à partir d'un seul.
Exemple :
Dans le triange IJK isocèle en I ci-dessous, on a :
= 104°. Quelle est la mesure de l'angle
?
=
car le triangle IJK est isocèle en I.
Donc
+ 2
= 180°.
Donc
= (180° - 104°) ÷ 2 = 76° ÷ 2 = 38° .
Angles d'un triangle isocèle rectangle :
Dans un triangle isocèle rectangle, les angles à la base mesurent 45°.
Exemple :
Dans le triange EFG isocèle rectangle en G ci-dessous, on a :
=
= 45° et
= 90°.
+ + = 45° + 45° + 90° = 180°
Angles d'un triangle équilatéral :
Dans un triangle équilatéral, les angles sont égaux et mesurent 60°.
Exemple :
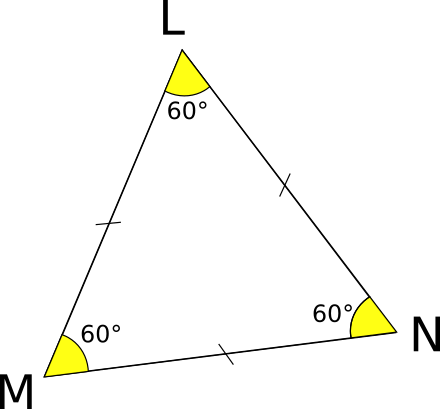
Dans le triange LMN équilatéral ci-dessous, on a :
=
=
= 60°.
