Cours de maths : Parallélogrammes particuliers
Le rectangle :
Un
rectangle est un quadrilatère qui a ses
quatre angles droits.
Exemple :
ABCD est un rectangle :

Un rectangle est un
parallélogramme particulier
Propriétés du rectangle :
Si un quadrilatère est un
rectangle, alors :
• ses diagonales se coupent en leur milieu et sont de même longueur
• ses côtés opposés sont parallèles et de même longueur
• les médiatrices de ses côtés sont des axes de symétrie
• le point d'intersection de ses diagonales est un centre de symétrie
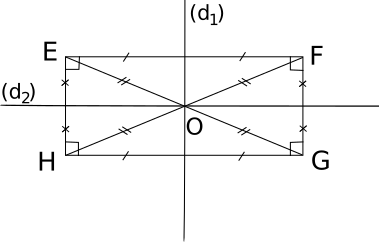
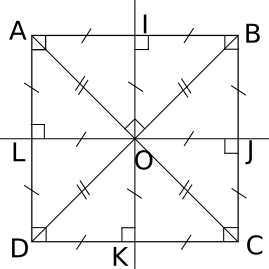
Exemple :
Reconnaître un rectangle :
• Si un quadrilatère a trois angles droits , alors c'est un rectangle
• Si un quadrilatère a ses diagonales de même longueur et qui se coupent en leur milieu , alors c'est un rectangle
• Si un parallélogramme a un angle droit, alors c'est un rectangle
• Si un parallélogramme a ses diagonales de même longueur, alors c'est un rectangle.
Le losange :
Un
losange est un quadrilatère qui a ses
quatre côtés de même longueur.
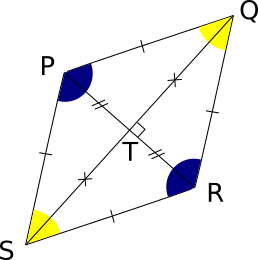
Exemple :
IJKL est un losange :
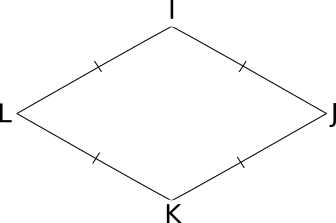
Un losange est un
parallélogramme particulier
Propriétés du losange :
Si un quadrilatère est un
losange, alors :
• ses diagonales se coupent en leur milieu et sont perpendiculaires
• ses côtés opposés sont parallèles et de même longueur
• ses angles opposés sont de même mesure
• ses diagonales sont des axes de symétrie
• le point d'intersection de ses diagonales est un centre de symétrie
Exemple :
Reconnaître un losange :
• Si un quadrilatère a ses quatre côtés de même longueur , alors c'est un losange
• Si un quadrilatère a ses diagonales perpendiculaires et qui se coupent en leur milieu , alors c'est un losange
• Si un parallélogramme a deux côtés consécutifs de même longueur, alors c'est un losange
• Si un parallélogramme a ses diagonales perpendiculaires, alors c'est un losange.
Le carré :
Un
carré est un quadrilatère qui a ses
quatre côtés de même longueur et ses
quatre angles droits .
Exemple :
ABCD est un carré :
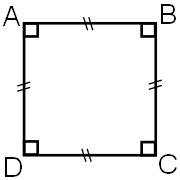
Un carré est un
parallélogramme particulier
Un carré est à la fois un
losange et un
rectangle.
Propriétés du carré :
Si un quadrilatère est un
carré, alors :
• ses diagonales se coupent en leur milieu, sont perpendiculaires et de même longueur
• ses côtés opposés sont parallèles et de même longueur
• ses diagonales et les médiatrices de ses côtés sont des axes de symétrie
• le point d'intersection de ses diagonales est un centre de symétrie
Exemple :
Reconnaître un carré :
• Si un quadrilatère a ses diagonales perpendiculaires, de même longueur et qui se coupent en leur milieu , alors c'est un carré
• Si un parallélogramme a ses diagonales perpendiculaires et de même longueur, alors c'est un carré
• Si un parallélogramme a deux côtés consécutifs perpendiculaires et de même longueur, alors c'est un carré
• Si un losange a un angle droit, alors c'est un carré
• Si un losange a des diagonales de même longueur, alors c'est un carré
• Si un rectangle a deux côtés consécutifs de même longueur, alors c'est un carré
• Si un rectangle a des diagonales perpendiculaires, alors c'est un carré.
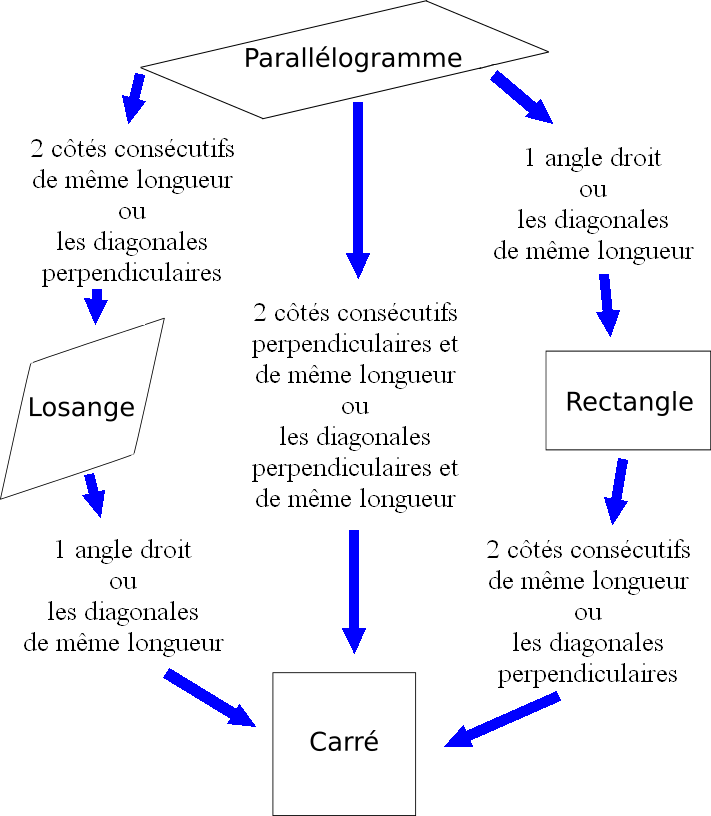
Résumé :
Comment obtenir un losange, un rectangle ou un carré à partir d'un parallélogramme :










====90°.