Cours : Intégration

Intégrale d'une fonction continue et positive

Définition :
Dans un repère orthogonal (O;

\vec{OI}

,

\vec{OJ}

),l'unité d'aire (notée u.a) est l'aire du rectangle OIKJ où K est le point de coordonnées (1;1).

Définition :
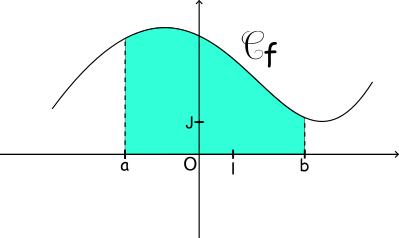
Soit f une fonction continue et positive sur un intervalle [a;b]. L'intégrale de a à b de la fonction f est l'aire, en unités d'aire, du domaine situé entre sa courbe, l'axe des abscisses et les droites d'équation x=a et x=b.
On la note

\int_{a}^{b} f (x) d x

.

Exemple :
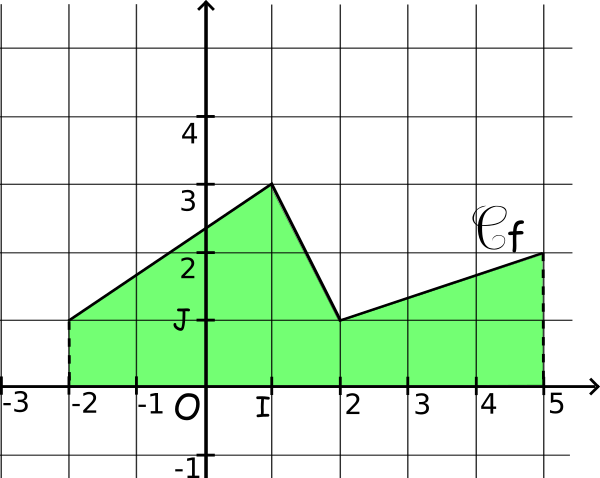
On a représenté ci-contre une fonction f définie sur l'intervalle [-2;5]. L'intégrale de -2 à 5 de la fonction f est l'aire du domaine situé entre sa courbe, l'axe des abscisses et les droites d'équation x=-2 et x=5. On peut compter que cette aire égale à 12 unités d'aires.
On a donc

\int_{-2}^{5} f (x) d x

=12.

Remarque :

Le nombre

\int_{a}^{b} f (x) d x

ne dépend que de f, a et b. On dit que x est une variable muette, on peut utiliser une autre lettre sans changer le résultat :

\int_{a}^{b} f (x) d x

=

\int_{a}^{b} f (t) d t

=

\int_{a}^{b} f (y) d y

= ...

Propriété immédiate :

\int_{a}^{a} f (x) d x = 0

Théorème fondamental : Soit f une fonction continue et positive sur un intervalle [a;b]. La fonction

F : x \mapsto \int_{a}^{x} f (t) d t

est la primitive de f sur [a;b] qui s'annule en a.

Propriété : Soit f une fonction continue et positive sur un intervalle [a;b] et F une primitive de f sur [a;b], Alors :

\int_{a}^{b} f (x) d x = F (b) - F (a)

Intégrale d'une fonction continue

Définition :
Soit f une fonction continue sur un intervalle [a;b]. L'intégrale de a à b de la fonction f est le nombre réel F(b) - F(a) où F est une primitive de f sur l'intervalle [a;b].
On la note

\int_{a}^{b} f (x) d x

ou encore

[F (x)] \begin{matrix} b \\ a \end{matrix}

\int_{a}^{b} f (x) d x

=

[F (x)] \begin{matrix} b \\ a \end{matrix}

=

F (b) - F (a)

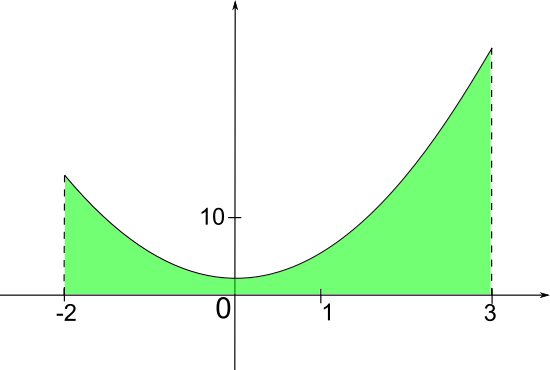
Exemple : Soit f la fonction définie sur [-2;3] par

f (x) = 3 x ² + 2

. Calculer I =

\int_{-2}^{3} f (x) d x

La fonction F définie par

F (x) = x^{3} + 2 x

est une primitive de f. Donc :
I =

\int_{-2}^{3} f (x) d x

I =

[F (x)] \begin{matrix} 3 \\ -2 \end{matrix}

I =

F (3) - F (-2)

I =

3^{3} + 2 \times 3 - ({(-2)}^{3} + 2 \times (-2))

I = 27 + 6 - (-8 - 4)
I = 33 - (-12) = 33 + 12 = 45.

Propriétés algébriques :
Soient f et g deux fonctions continues sur un intervalle I. Soient a, b et c trois réels appartenant à cet intervalle et k un nombre réel.

Inversion des bornes :

•

\int_{a}^{b} f (x) d x

=

- \int_{b}^{a} f (x) d x

Relation de Chasles :

•

\int_{a}^{b} f (x) d x

=

\int_{a}^{c} f (x) d x

+

\int_{c}^{b} f (x) d x

Linéarité de l'intégration :

•

\int_{a}^{b} (f + g) (x) d x

=

\int_{a}^{b} f (x) d x

+

\int_{a}^{b} g (x) d x

•

\int_{a}^{b} k f (x) d x

=

k \int_{a}^{b} f (x) d x

Intégrales et inégalités :
Soient a, b deux réels tels que a≤b et f et g deux fonctions continues sur l'intervalle [a;b].

Positivité :

• Si, pour tout nombre réel x appartenant à [a;b], f(x)≥0, alors

\int_{a}^{b} f (x) d x \geq 0

• Si, pour tout nombre réel x appartenant à [a;b], f(x)≤0, alors

\int_{a}^{b} f (x) d x \leq 0

Ordre :

• Si, pour tout nombre réel x appartenant à [a;b], g(x)≤f(x), alors

\int_{a}^{b} g (x) d x \leq \int_{a}^{b} f (x) d x

Intégration par parties :
Soient f et g deux fonctions dérivables sur un intervalle I telles que f' et g' soient continues sur I et a et b deux réels appartenant à I. On a:

\int_{a}^{b} f' (x) g (x) d x

=

[f (x) g (x)] \begin{matrix} b \\ a \end{matrix}

-

\int_{a}^{b} f (x) g' (x) d x

Exemple : Calculer I =

\int_{0}^{1} x e^{x} d x

.

Soit f et g deux fonctions définies sur [0;1] par

g (x) = x

et

f (x) = e^{x}

. On a donc

g' (x) = 1

et

f' (x) = e^{x}

. f' et g' sont continues sur [0;1], on a donc:
I =

\int_{0}^{1} x e^{x} d x

=

\int_{0}^{1} g (x) f' (x) d x

=

[f (x) g (x)] \begin{matrix} 1 \\ 0 \end{matrix}

-

\int_{0}^{1} g' (x) f (x) d x

Donc I =

[x e^{x}] \begin{matrix} 1 \\ 0 \end{matrix}

-

\int_{0}^{1} e^{x} d x

Donc I =

e^{1}

-

[e^{x}] \begin{matrix} 1 \\ 0 \end{matrix}

=

e

-

(e^{1} - e^{0})

=

e

-

(e - 1)

=1

Application au calcul d'aire

Cas d'une fonction négative :
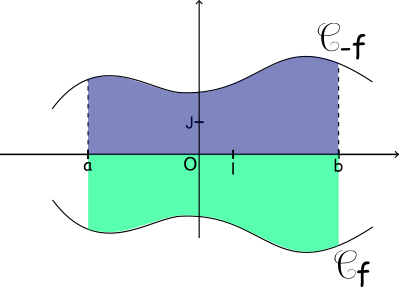
Soit f une fonction continue et négative sur un intervalle [a;b]. L'aire, en unités d'aire, du domaine situé entre sa courbe, l'axe des abscisses et les droites d'équation x=a et x=b est égale à -

\int_{a}^{b} f (x) d x

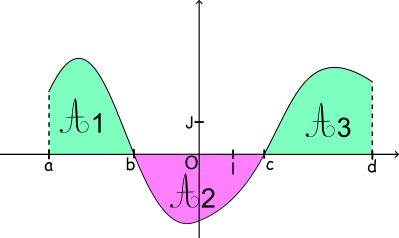
Cas d'une fonction de signe non constant :
Dans le cas d'une fonction de signe non constant, il faut d'abord étudier le signe de la fonction pour pouvoir calculer les aires. Dans l'exemple ci-contre : l'aire totale est égale à la somme des trois aires.
A = A1 + A2 + A3.
A =

\int_{a}^{b} f (x) d x

-

\int_{b}^{c} f (x) d x

+

\int_{c}^{d} f (x) d x

integrale fonction de signe non constant

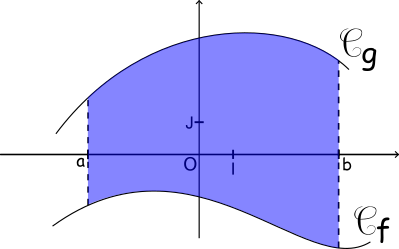
Aire entre deux courbes :
Soit f et g deux fonctions continues sur un intervalle [a;b] telles que f(x)≤g(x) pour tout x appartenant à l'intervalle [a;b]. L'aire, en unités d'aire, du domaine situé entre les courbes représentatives de f et g, et les droites d'équation x=a et x=b est égale à

\int_{a}^{b} (g (x) - f (x)) d x

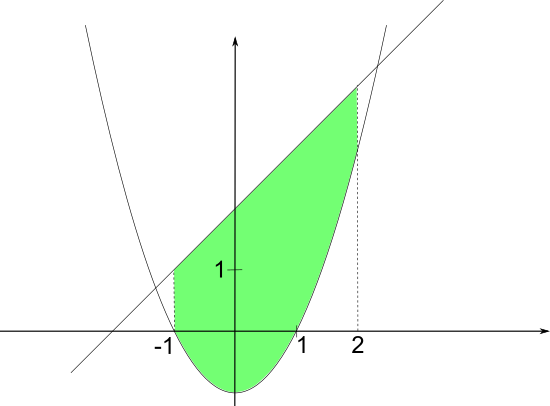
Exemple : Soient f et g les fonctions définies sur [-1;2] par

f (x) = x + 2

et

g (x) = x ² - 1

.
Calculer l'aire du domaine compris entre les courbes représentatives de f et de g et les droites d'équations x=-1 et x=2.

1) Etude du signe de f(x)-g(x) sur [-1;2]

f (x) - g (x) = - x ² + x + 3

a=-1, b=1 et c =3 donc Δ=1²-4×(-1)*3=13. Δ>0 donc l'équation f(x)-g(x)=0 admet deux solutions

x_{1} = \frac{-b - \sqrt{Δ}}{2 a} = \frac{-1 - \sqrt{13}}{-2} \approx 2,3

>2 et

x_{2} = \frac{-b + \sqrt{Δ}}{2 a} = \frac{-1 + \sqrt{13}}{-2} \approx -1,3

< -1.
a<0 donc f(x)-g(x) ≥ 0 pour x compris entre

x_{1}

et

x_{2}

donc f(x)-g(x)≥0 sur [-1;2]

2) Calcul de l'aire
L'aire du domaine compris entre les courbes représentatives de f et de g et les droites d'équations x=-1 et x=2 est donc égale à

\int_{-1}^{2} f (x) - g (x) d x

.
La fonction

x \mapsto - \frac{x^{3}}{3} + \frac{x^{2}}{2} + 3 x

est une primitive de f-g. Donc :

\int_{-1}^{2} f (x) - g (x) d x

=

[- \frac{x^{3}}{3} + \frac{x^{2}}{2} + 3 x] \begin{matrix} 2 \\ -1 \end{matrix}

=

\frac{-8}{3} + 2 + 6 - (\frac{1}{3} + \frac{1}{2} - 3)

=

\frac{-8}{3} + 8 - \frac{1}{3} - \frac{1}{2} + 3

=

8 - \frac{1}{2}

=

\frac{15}{2}

Valeur moyenne

Définition :
Soit f une fonction continue sur un intervalle [a;b]. La valeur moyenne de f sur [a;b] est le nombre m tel que

m = \frac{1}{b - a} \int_{a}^{b} f (x) d x

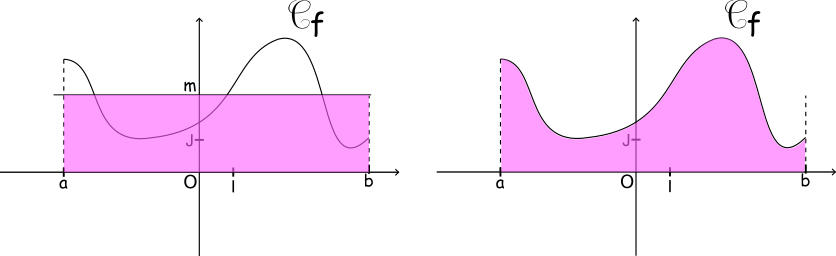
Interprétation graphique :
Si f est une fonction positive, l'aire sous la courbe est égale à l'aire du rectangle de largeur b-a et de hauteur m.

Exemple : Soit f la fonction définie sur ℝ par

f (x) = e^{x} + 1

. Calculer la valeur moyenne de f sur l'intervalle [0;5].
La fonction F définie sur ℝ par

F (x) = e^{x} + x

est une primitive de f, donc :

\int_{0}^{5} f (x) d x

=

[e^{x} + x] \begin{matrix} 5 \\ 0 \end{matrix}

=

e^{5} + 5 - (e^{0} + 0)

=

e^{5} + 5 - 1

=

e^{5} + 4

Donc la valeur moyenne m de f sur l'intervalle [0;5] est égale à

\frac{e^{5} + 4}{5}