Fonctions continues
Définition :
Soit
f une fonction définie sur un intervalle
I et
a un réel appartenant à I.
• La fonction
f est
continue en
a si
.
• La fonction
est
continue sur
I si
est continue pour tout réel
de
I
Exemples :
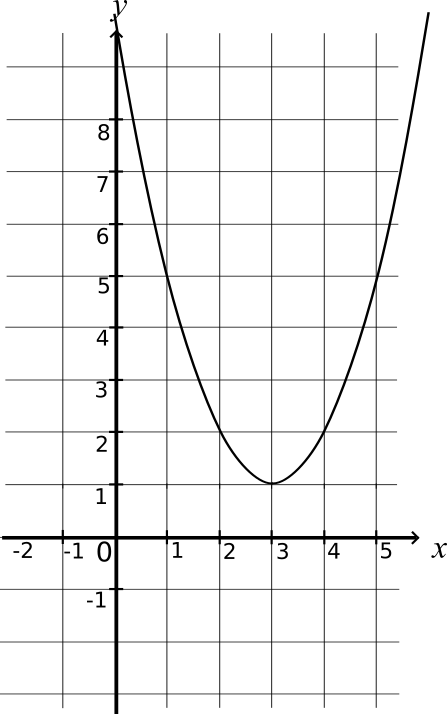 Représentation graphique de la fonction f définie sur ℝ par :
Représentation graphique de la fonction f définie sur ℝ par :
f(x) = x² - 6x + 10
f est continue sur ℝ
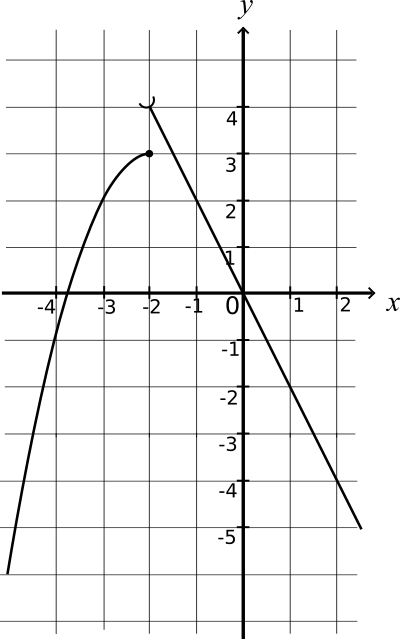 Représentation graphique de la fonction f définie sur ℝ par :
f
Représentation graphique de la fonction f définie sur ℝ par :
f n'est pas continue en -2, donc
f n'est pas continue sur ℝ
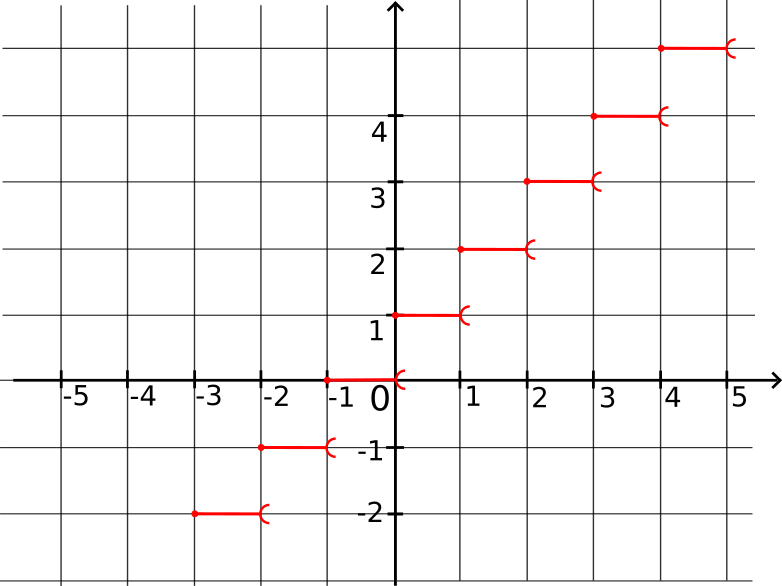 Représentation graphique de la fonction partie entière
f
Représentation graphique de la fonction partie entière
f n'est pas continue sur ℝ
Propriétés :
• Les fonctions affines, les fonctions polynômes, la fonction racine carrée et la fonction exponentielle sont continues sur leur ensemble de définition.
• Les sommes, produits, quotients et composées de fonctions continues sont continues sur tout intervalle de leur ensemble de définition.
• Une fonction dérivable sur un intervalle est continue sur cet intervalle.
Exemple :
Soit
f la fonction définie sur ]-∞;4[ ∪ ]4;+∞[ par
est continue sur ]-∞;4[ et est continue sur ]4;+∞[.
Remarque :
Une fonction continue sur un intervalle n'est pas toujours dérivable sur cet intervalle. Par exemple, la fonction valeur absolue est continue en 0 mais n'est pas dérivable en 0.
Propriété :
Soit
f une fonction continue sur un intervalle
I, (U
n) une suite à valeurs dans
I et
a un réel appartenant à
I.
Si (U
n) converge vers
a, alors (
f(U
n)) converge vers
f(
a)
Exemple :
Soit (U
n) la suite définie par U
0=9 et U
n+1=
pour tout entier n≥0. (U
n) est décroissante et minorée par 1 donc (U
n) est convergente. (
voir démonstration).
Soit
l la limite de (U
n). La fonction racine carrée est continue sur [0;+∞[, donc
converge vers
. Or, (U
n+1) =
et par unicité de la limite,
l est solution de l'équation
.
⇔
=
et
≥0
⇔
= 0 ou
= 1
Or (U
n) est minorée par 1, donc
l=1.
Théorème des valeurs intermédiaires
Théorème (cas général) :
Soit
f une fonction
continue sur un intervalle [
a;
b] où
a et
b sont deux réels tels que
a<
b.
Pour tout réel
k compris entre
f(a) et
f(b), il existe un réel
c de l'intervalle [
a;
b] tel que
f(c) = k.
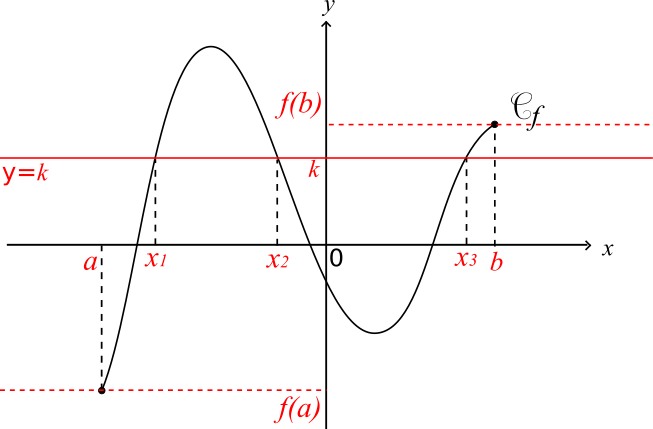
Illustration :
f est continue sur l'intervalle [a;b]
k ∈ [f(a);f(b)]
L'équation = k a trois solutions dans l'intervalle [a;b] : , et .
Exemple :
Soit
la fonction définie sur [0;+∞[ par
=
. Montrer que l'équation
= 5 admet au moins une solution dans l'intervalle [0;4]
Solution :La fonction
est continue sur [0;4] comme somme de fonctions continues.
=
= 0 et
=
= 16-6 = 10 , donc 5 ∈ [
(0);
(4)].
D'après le théorème des valeurs intermédiaires, l'équation
= 5 admet au moins une solution dans l'intervalle [0;4].
Théorème (cas d'une fonction strictement monotone) :
Soit
f une fonction
continue et strictement monotone sur un intervalle [
a;
b] où
a et
b sont deux réels tels que
a<
b.
Pour tout réel
k compris entre
f(a) et
f(b), il existe un
unique réel
c de l'intervalle [
a;
b] tel que
f(c) = k.
Illustrations :
Cas n°1
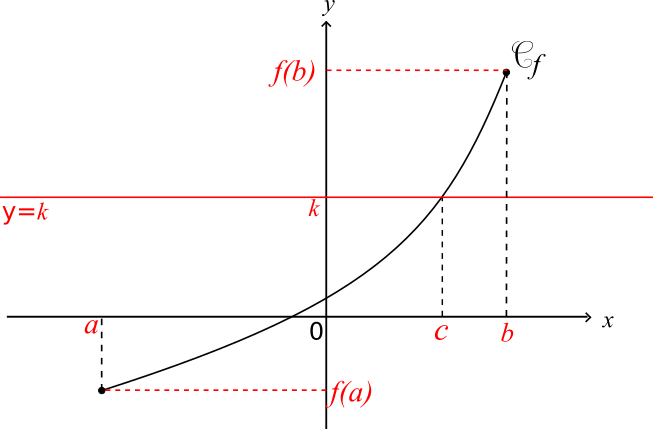
f est continue et strictement croissante sur l'intervalle [a;b]
k ∈ [f(a);f(b)]
L'équation f(x) = k a une unique solution c appartenant à l'intervalle [a;b]
Cas n°2
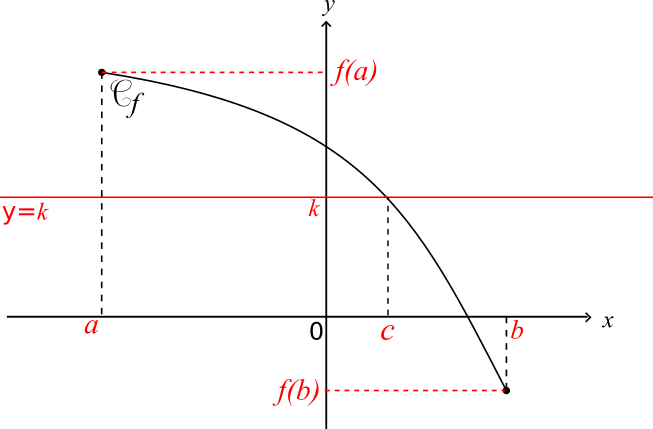
f est continue et strictement décroissante sur l'intervalle [a;b]
k ∈ [f(b);f(a)]
L'équation f(x) = k a une unique solution c appartenant à l'intervalle [a;b]
Exemple :
Soit
la fonction définie sur [0;+∞[ par
=
. Montrer que l'équation
= 3 admet une unique solution dans l'intervalle [0;1]
Solution :La fonction
est continue et dérivable sur [0;1] comme somme de fonctions continues et dérivables.
=
.
> 0 pour tout
∈ [0;1] donc
est strictement croissante sur [0;1]
=
= 1 - 1 = 0
=
= e + 3 , donc 3 ∈ [
(0);
(1)].
D'après le théorème des valeurs intermédiaires, l'équation
= 3 admet une unique solution dans l'intervalle [0;1].
Remarque : Le théorème des valeurs intermédiaires s'applique aussi sur un intervalle ouvert ou semi-ouvert. Si une borne de l'intervalle est ouverte, alors on considère la limite de
f en cette borne.
Exemple :
Soit
la fonction définie sur ℝ par
=
. Montrer que l'équation
= 0 admet une unique solution sur ℝ
Solution :La fonction
est continue et dérivable sur ℝ comme somme de fonctions continues et dérivables.
=
.
< 0 pour tout
∈ ℝ donc
est strictement décroissante sur ℝ
, donc
< 0 <
D'après le théorème des valeurs intermédiaires, l'équation
= 0 admet une unique solution sur ℝ.